题目内容
9.下列说法正确的是( )| A. | 从独立性检验可知有99%的把握认为吃地沟油与患肠胃癌有关系时,我们说某人吃地沟油,那么他有99%的可能患肠胃癌 | |
| B. | 回归直线不一定过样本中心点($\overline{x}$,$\overline{y}$) | |
| C. | 相关系数-1≤r≤1.r越大,线性相关的关系越强 | |
| D. | 用样本研究变量间的相关关系,求得回归直线方程为y=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,回归系数为r,若$\stackrel{∧}{b}$>0,则r>0 |
分析 在一个独立性检验中,我们有99%的把握认为吃地沟油与患肠胃癌有关系时,这一句话的意思是有99%的把握认为这个推理是正确的,有1%的可能性认为推理出现错误,由此判断A;直接由回归直线一定过样本中心点($\overline{x}$,$\overline{y}$)判断B;由|r|越大,线性相关的关系越强判断C;直接利用回归直线方程的相关性,通过直线的斜率,即可判断选项D.
解答 解:从独立性检验可知,我们有99%的把握认为吃地沟油与患肠胃癌有关系时,这一句话的意思是有99%的把握认为这个推理是正确的,有1%的可能性认为推理出现错误,并不是说吃地沟油,那么他有99%的可能患肠胃癌,故A错误;
回归直线一定过样本中心点($\overline{x}$,$\overline{y}$),故B错误;
相关系数-1≤r≤1.|r|越大,线性相关的关系越强,故C错误;
由回归直线方程的相关性可知,当$\stackrel{∧}{b}$>0时,回归直线方程是正相关,则r>0,故D正确.
故选:D.
点评 本题考查命题的真假判断与应用,考查了学生对教材基础知识的理解与掌握,是基础题.

练习册系列答案
相关题目
19.已知数列{xn}满足lgxn+1=1+lgxn(n∈N*),且x1+x2+x3+…+x100=100,则lg(x101+x102+…+x200)的值为( )
| A. | 102 | B. | 101 | C. | 100 | D. | 99 |
20.若f(x)=xlnx,则f′(e)=( )
| A. | 0 | B. | 1 | C. | 2 | D. | e |
17.过点P(2,-1)作圆(x-1)2+y2=25的弦AB,则弦长AB的最短时AB所在的直线方程方程是( )
| A. | x-y-3=0 | B. | 2x+y-3=0 | C. | x+y-1=0 | D. | 2x-y-5=0 |
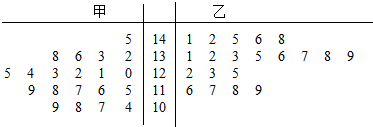
14.为了研究“教学方式”对教学质量的影响,某高中英语老师分别用两种不同的教学方法对入学英语平均分和优秀率都相同的甲乙两个高一新班进行教学(勤奋程度和自觉性相同),以下茎叶图为甲乙两班(每班均20人)学生的英语期末成绩,若成绩不低于125分的为优秀,填写下面的2×2列联表,并判断是否有97.5%的把握认为“成绩优秀与教学方式有关”.
参考公式:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{{n}_{+2}}^{\;}}$
附表:

| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 非优秀 | |||
| 合计 |
附表:
| P(X2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
18.与向量$\overrightarrow{a}$=(2,2)方向相同的单位向量是( )
| A. | ($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$) | B. | (1,1) | C. | (-1,-1) | D. | ($\frac{1}{2}$,$\frac{1}{2}$) |
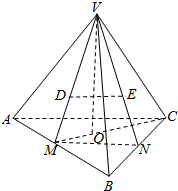 如图所示,已知D,E分别是三棱锥V-ABC的两个侧面VAB,VBC的重心.
如图所示,已知D,E分别是三棱锥V-ABC的两个侧面VAB,VBC的重心.