题目内容
设圆内两条相交弦，其中一弦长为8 cm，且被交点平分，另一条弦被交点分成1∶4两部分，则这条弦长是
A．2 cm B．8 cm C．10 cm D．12 cm
C
【解析】由相交弦推论即可得．
设另一条弦被分成x cm，
4x cm.则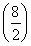
2＝x·4x，所以x＝2 cm.
所以弦长为10 cm.
练习册系列答案
相关题目
题目内容
设圆内两条相交弦，其中一弦长为8 cm，且被交点平分，另一条弦被交点分成1∶4两部分，则这条弦长是
A．2 cm B．8 cm C．10 cm D．12 cm
C
【解析】由相交弦推论即可得．
设另一条弦被分成x cm，
4x cm.则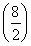2＝x·4x，所以x＝2 cm.
所以弦长为10 cm.
