题目内容
过点C(0,1)的椭圆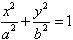 (a>b>0)的离心率为
(a>b>0)的离心率为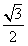 ,椭圆与x轴交于两点A(a,0)、A(-a,0),过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q。
,椭圆与x轴交于两点A(a,0)、A(-a,0),过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q。
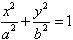 (a>b>0)的离心率为
(a>b>0)的离心率为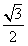 ,椭圆与x轴交于两点A(a,0)、A(-a,0),过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q。
,椭圆与x轴交于两点A(a,0)、A(-a,0),过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q。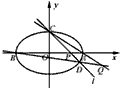
(Ⅰ)当直线l过椭圆右焦点时,求线段CD的长;
(Ⅱ)当点P异于点B时,求证: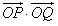 为定值。
为定值。
(Ⅱ)当点P异于点B时,求证:
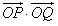 为定值。
为定值。解:(Ⅰ)由已知得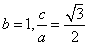 ,解得
,解得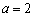
所以椭圆方程为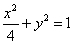
椭圆的右焦点为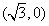 ,此时直线的方程为
,此时直线的方程为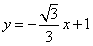 代入椭圆方程得
代入椭圆方程得
解得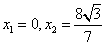 ,代入直线l的方程得
,代入直线l的方程得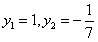
所以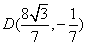
故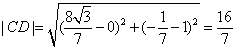 ;
;
(Ⅱ)当直线l与x轴垂直时与题意不符
设直线l的方程为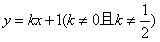 ,代入椭圆方程得
,代入椭圆方程得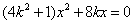
解得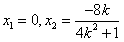 ,代入直线l的方程得
,代入直线l的方程得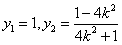
所以D点的坐标为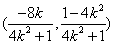
又直线AC的方程为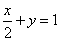 ,又直线BD的方程为
,又直线BD的方程为 ,联立得
,联立得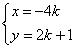
因此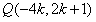 ,又
,又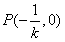
所以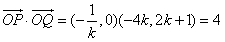
故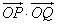 为定值。
为定值。
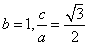 ,解得
,解得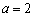
所以椭圆方程为
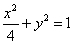
椭圆的右焦点为
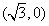 ,此时直线的方程为
,此时直线的方程为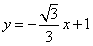 代入椭圆方程得
代入椭圆方程得
解得
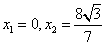 ,代入直线l的方程得
,代入直线l的方程得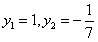
所以
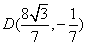
故
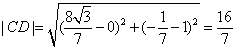 ;
;(Ⅱ)当直线l与x轴垂直时与题意不符
设直线l的方程为
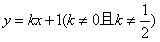 ,代入椭圆方程得
,代入椭圆方程得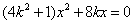
解得
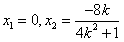 ,代入直线l的方程得
,代入直线l的方程得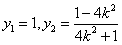
所以D点的坐标为
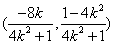
又直线AC的方程为
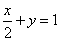 ,又直线BD的方程为
,又直线BD的方程为 ,联立得
,联立得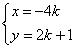
因此
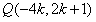 ,又
,又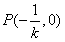
所以
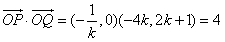
故
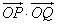 为定值。
为定值。
练习册系列答案
相关题目
