题目内容
已知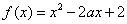 .
.
(Ⅰ) 若不等式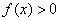 在区间
在区间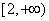 上恒成立,求实数
上恒成立,求实数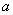 的取值范围;
的取值范围;
(Ⅱ) 解关于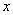 的不等式
的不等式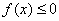 .
.
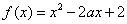 .
.(Ⅰ) 若不等式
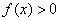 在区间
在区间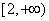 上恒成立,求实数
上恒成立,求实数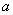 的取值范围;
的取值范围;(Ⅱ) 解关于
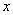 的不等式
的不等式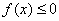 .
.(1)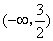 (2){x|a-
(2){x|a-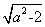 ≤x≤a+
≤x≤a+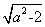 }.
}.
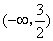 (2){x|a-
(2){x|a-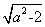 ≤x≤a+
≤x≤a+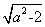 }.
}.试题分析:解: (Ⅰ)
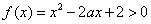 在区间
在区间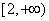 上恒成立,即
上恒成立,即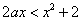 ,
,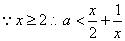 , 2分
, 2分令
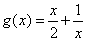 ,
,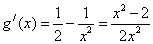 ,
,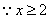 ,
,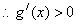 ,
,所以g(x)在
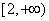 上是增函数,
上是增函数,所以g(x)的最小值是
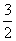 .
.则实数
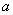 的取值范围是
的取值范围是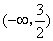 . 5分
. 5分(Ⅱ)∵Δ=4a2-8,
∴当Δ<0,即-
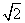 <a<
<a<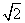 时,
时,原不等式对应的方程无实根,原不等式的解集为
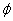 ; 6分
; 6分当Δ=0,即a=±
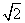 时,原不等式对应的方程有两个相等实根.
时,原不等式对应的方程有两个相等实根.当a=
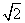 时,原不等式的解集为{x|x=
时,原不等式的解集为{x|x=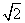 },
},当a=-
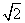 时,原不等式的解集为{x|x=-
时,原不等式的解集为{x|x=-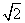 }; 8分
}; 8分当Δ>0,即a>
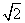 或a<-
或a<-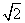 时,原不等式对应的方程有两个不等实根,分别为x1=a-
时,原不等式对应的方程有两个不等实根,分别为x1=a-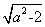 ,x2=a+
,x2=a+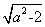 ,且x1<x2,
,且x1<x2,∴原不等式的解集为{x|a-
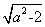 ≤x≤a+
≤x≤a+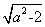 }. 11分
}. 11分综上,当-
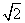 <a<
<a<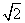 时, 不等式的解集为
时, 不等式的解集为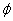 ;当a=
;当a=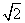 时,不等式的解集为
时,不等式的解集为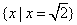 };当a=-
};当a=-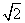 时,不等式的解集为{x|x=-
时,不等式的解集为{x|x=-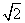 };当a>
};当a>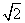 或a<-
或a<-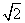 时,不等式的解集为{x|a-
时,不等式的解集为{x|a-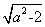 ≤x≤a+
≤x≤a+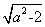 }. 12分
}. 12分点评:主要是考查了二次函数的性质以及二次不等式求解,属于中档题。

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 的解集。
的解集。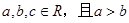 ,则下列不等式一定成立的是 ( )
,则下列不等式一定成立的是 ( )



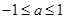 时,不等式
时,不等式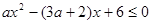 恒成立,求实数
恒成立,求实数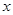 的取值范围
的取值范围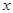 的不等式
的不等式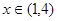 时,不等式
时,不等式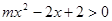 恒成立,则m的取值范围是__ __.
恒成立,则m的取值范围是__ __.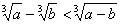 成立,则
成立,则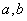 应满足的条件是
应满足的条件是 且
且
 且
且
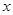 的不等式
的不等式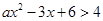 , -(*)
, -(*)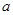 的取值范围;
的取值范围;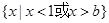 ,求不等式
,求不等式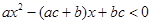 的解集.
的解集.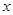 的不等式
的不等式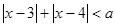 ,
,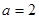 时,解上述不等式;
时,解上述不等式;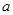 的取值范围。
的取值范围。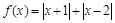 ,不等式
,不等式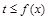 在
在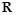 上恒成立.
上恒成立.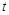 的取值范围;
的取值范围;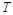 ,若正实数
,若正实数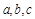 满足
满足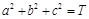 ,求
,求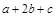 的最大值.
的最大值.