Question

【题目】已知函数f（x）＝ax3＋bx2＋cx在x＝±1处取得极值，在x＝0处的切线与直线3x＋y＝0平行．

（1）求f（x）的解析式；

（2）已知点A（2，m），求过点A的曲线y＝f（x）的切线条数．

Answer 1

【答案】（1）f（x）＝x3－3x；（2）①当m>2或m<－6时，方程m＝－2t3＋6t2－6只有一解，即过点A只有一条切线；②当m＝2或m＝－6时，方程m＝－2t3＋6t2－6恰有两解，即过点A有两条切线；③当－6<m<2时，方程m＝－2t3＋6t2－6有三解，即过点A有三条切线．

【解析】

试题分析：（1）求导，利用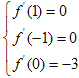进行求解；（2）设出切点坐标，利用导数的几何意义求其斜率，写出切线方程，构造函数，利用导数研究极值，再通过数形结合思想求解．

试题解析：（1）f′（x）＝3ax2＋2bx＋c，

由题意可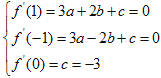得解得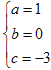所以f（x）＝x3－3x．

（2）设切点为（t，t3－3t），由（1）知f′（x）＝3x2－3，所以切线斜率k＝3t2－3，

切线方程为y－（t3－3t）＝（3t2－3）（x－t）．

又切线过点A（2，m），代入得m－（t3－3t）＝（3t2－3）（2－t），解得m＝－2t3＋6t2－6．

设g（t）＝－2t3＋6t2－6，令g′（t）＝0，即－6t2＋12t＝0，解得t＝0或t＝2．

当t变化时，g′（t）与g（t）的变化情况如下表：

t	（－∞，0）	0	（0,2）	2	（2，＋∞）
g′（t）	－	0	＋	0	－
g（t）	↘	极小值	↗	极大值	↘

所以g（t）的极小值为g（0）＝－6，极大值为g（2）＝2．

p>作出函数草图可知：

①当m>2或m<－6时，方程m＝－2t3＋6t2－6只有一解，即过点A只有一条切线；

②当m＝2或m＝－6时，方程m＝－2t3＋6t2－6恰有两解，即过点A有两条切线；

③当－6<m<2时，方程m＝－2t3＋6t2－6有三解，即过点A有三条切线．