题目内容
17.已知f(x)=lnx+$\frac{1}{x}$,且2<p<q.,求证:对于x∈(p,q),有$\frac{f(x)-f(p)}{x-p}$>$\frac{f(x)-f(q)}{x-q}$.分析 先求导,利用导数判断出函数f(x)的单调性,得到f(x)在(2,+∞)上单调递增,分别设A点的坐标为(x,f(x)),B为(p,f(p)),C(q,f(q)),利用斜率即可证明.
解答 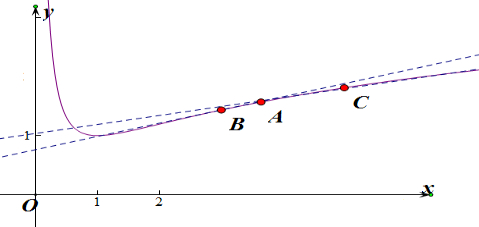 解:∵f(x)=lnx+$\frac{1}{x}$,
解:∵f(x)=lnx+$\frac{1}{x}$,
∴f′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$,
令f′(x)=0,解得x=1,
∴f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∵2<p<q,
∴f(x)在(2,+∞)上单调递增,
如图所示,
设A点的坐标为(x,f(x)),B为(p,f(p)),C(q,f(q)),
则kAB=$\frac{f(x)-f(p)}{x-p}$,kAC=$\frac{f(x)-f(q)}{x-q}$.
由图象可知kAB>kAC,
∴对于x∈(p,q),有$\frac{f(x)-f(p)}{x-p}$>$\frac{f(x)-f(q)}{x-q}$.
点评 本题考查导数和函数单调性的关系,以及有关直线的斜率问题,属于中档题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
8.空间直角坐标系中,已知原点为O,A(1,0,0),B(0,1,0),C(0,0,1),在三棱锥O-ABC中任取一点P(x,y,z),则满足$\sqrt{{x^2}+{y^2}+{z^2}}≤\frac{1}{2}$的概率是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{10}$ |
12.已知等差数列{an}前n项和为Sn,a4=2,S10=10,则a7的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |