题目内容
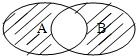 设函数f(x)=lg(1-x2) 集合A={x|y=f(x)},B={y|y=f(x)},则图中阴影部分表示的集合为
设函数f(x)=lg(1-x2) 集合A={x|y=f(x)},B={y|y=f(x)},则图中阴影部分表示的集合为考点:Venn图表达集合的关系及运算
专题:计算题,集合
分析:由题意,化简集合A,B,再由图象求集合.
解答:
解:A={x|y=f(x)}=(-1,1),
B={y|y=f(x)}=(-∞,0],
故图中阴影部分表示的集合为
(-∞,-1]∪(0,1);
故答案为:(-∞,-1]∪(0,1).
B={y|y=f(x)}=(-∞,0],
故图中阴影部分表示的集合为
(-∞,-1]∪(0,1);
故答案为:(-∞,-1]∪(0,1).
点评:本题考查了集合的化简与运算,属于基础题.

练习册系列答案
相关题目
设x,y满足约束条件
,则目标函数z=2x+y的最大值为( )
|
| A、-6 | ||
B、-
| ||
C、
| ||
| D、6 |
函数y=sin2x+sinx-1的值域为( )
| A、[-1,1] | ||
B、[-
| ||
C、[-
| ||
D、[-1,
|
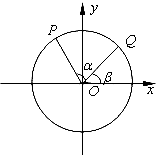 如图,以ox轴为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P,Q,已知点P的坐标为(-
如图,以ox轴为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P,Q,已知点P的坐标为(-