Question

如图，设A、B、C、D为球O上四点，若AB、AC、AD两两互相垂直，且AB=AC=

6

， AD=2，则OD与平面ABC所成的角为

 

．

Answer 1

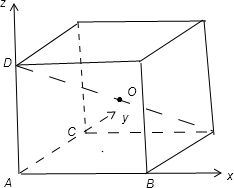
分析：由题意把图形特殊化为长方体的一部分的三条侧棱两两垂直的三棱锥，由于知道各个棱长，所以可以通过建立空间直角坐标系，利用空间向量的知识把线面角的求解转化为直线的法向量与平面的法向量之间的夹角的方法求解即可．

解答：解：由题意及图形，可以把图形化并建立如图的空间直角坐标系：∵AB、AC、AD两两互相垂直，且AB=AC=

6

， AD=2
∴A（0，0，0）  B(

6

，0，0)   C(

6

，0，0)  D(0，0，2) O( 

6

2

 ，

6

2

，1) 而平面ABC的法向量取

AD

=(0，0，2)  直线的方向向量取

DO

=(

6

2

，

6

2

，-1)则  cos＜

AD

，

DO

＞=-

1

2

，所以OD与平面ABC所成的线面角的正弦为

1

2

，所以OD与平面所成的角为

π

6

．
  故答案为：

π

6

点评：此题重点考查上了立体几何做题时的特殊模型及空间向量的解题的方法，还考查了直线与平面所成角的概念及做题时把问题等价转化的思想．