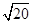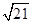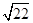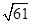题目内容
下面的一组图形为某一四棱锥S-ABCD的底面与侧面。

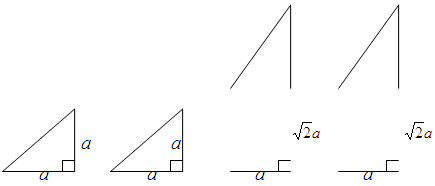
(1)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说明理由;
(2)若SA 面ABCD,E为AB中点,求证:面
面ABCD,E为AB中点,求证:面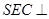 面
面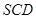
(3)求点D到面SEC的距离。

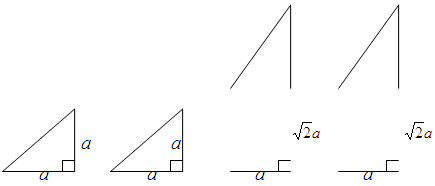
(1)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说明理由;
(2)若SA
 面ABCD,E为AB中点,求证:面
面ABCD,E为AB中点,求证:面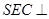 面
面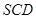
(3)求点D到面SEC的距离。
(1)见解析(2)见解析(3)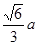
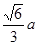
本题考查线面垂直、面面垂直定义,判定,性质.以及空间距离的求解.平面问题与空间问题相互转化的思想方法,考查计算能力
(1)由 SA⊥AB,SA⊥AD 可得,存在一条侧棱SA垂直于底面
(2)分别取SC、SD的中点G、F,可证AF∥EG.证明CD⊥AF,AF⊥SD,从而证明 AF⊥面SCD,故EG⊥面SCD,从而证得面SEC⊥面SCD.
(3)由面面垂直的性质定理,由A向平面SAC与平面SBD的交线作垂线,构造直角三角形解决点A到平面SBD的距离
解(1)存在一条侧棱垂直于底面(如图)

即SA 底面ABCD………………3分
底面ABCD………………3分
∵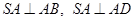 ,且AB、AD是面ABCD内两条相交直线
,且AB、AD是面ABCD内两条相交直线
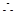 SA
SA 底面ABCD……………………5分
底面ABCD……………………5分
(2)分别取SC、SD的中点G、F,连GE、GF、FA,
则GF//EA,GF=EA,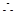 AF//EG
AF//EG
而由SA 面ABCD得SA
面ABCD得SA CD,
CD,
又AD CD,
CD,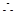 CD
CD 面SAD,
面SAD,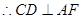
又SA=AD,F是中点,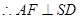
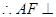 面SCD,即EG
面SCD,即EG 面SCD,
面SCD,
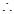 面
面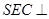 面
面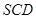 …………10分
…………10分
(3)作DH SC于H,
SC于H,
∵面SEC 面SCD,
面SCD,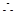 DH
DH 面SEC,
面SEC,
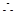 DH之长即为点D到面SEC的距离,12分
DH之长即为点D到面SEC的距离,12分
在Rt SCD中,
SCD中,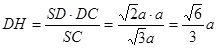
答:点D到面SEC的距离为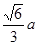 …………14分
…………14分
(1)由 SA⊥AB,SA⊥AD 可得,存在一条侧棱SA垂直于底面
(2)分别取SC、SD的中点G、F,可证AF∥EG.证明CD⊥AF,AF⊥SD,从而证明 AF⊥面SCD,故EG⊥面SCD,从而证得面SEC⊥面SCD.
(3)由面面垂直的性质定理,由A向平面SAC与平面SBD的交线作垂线,构造直角三角形解决点A到平面SBD的距离
解(1)存在一条侧棱垂直于底面(如图)

即SA
 底面ABCD………………3分
底面ABCD………………3分∵
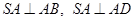 ,且AB、AD是面ABCD内两条相交直线
,且AB、AD是面ABCD内两条相交直线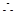 SA
SA 底面ABCD……………………5分
底面ABCD……………………5分(2)分别取SC、SD的中点G、F,连GE、GF、FA,
则GF//EA,GF=EA,
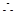 AF//EG
AF//EG而由SA
 面ABCD得SA
面ABCD得SA CD,
CD,又AD
 CD,
CD,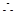 CD
CD 面SAD,
面SAD,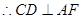
又SA=AD,F是中点,
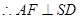
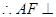 面SCD,即EG
面SCD,即EG 面SCD,
面SCD, 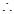 面
面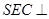 面
面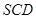 …………10分
…………10分(3)作DH
 SC于H,
SC于H,∵面SEC
 面SCD,
面SCD,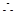 DH
DH 面SEC,
面SEC,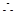 DH之长即为点D到面SEC的距离,12分
DH之长即为点D到面SEC的距离,12分在Rt
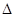 SCD中,
SCD中,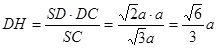
答:点D到面SEC的距离为
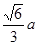 …………14分
…………14分
练习册系列答案
相关题目
 a(0<
a(0<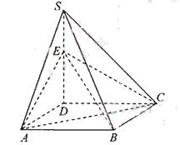
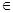 (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE: ,高为
,高为 ,则圆锥的侧面积是
,则圆锥的侧面积是  .
.
 的面积为8,当矩形周长取最小值时,沿对角线
的面积为8,当矩形周长取最小值时,沿对角线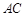 把
把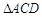 折起,则三棱锥
折起,则三棱锥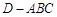 的外接球的表面积为________
的外接球的表面积为________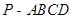 中,底面
中,底面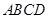 是矩形,
是矩形,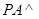 平面
平面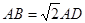 是线段
是线段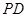 上的点,
上的点,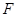 是线段
是线段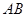 上的点,且
上的点,且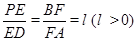
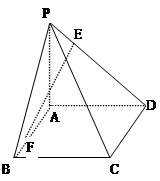
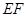 与平面
与平面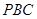 的关系,并证明;
的关系,并证明;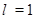 时,证明:面
时,证明:面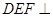 平面
平面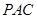 .
.