题目内容
设等差数列 的前
的前 项和为
项和为 .且
.且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,数列
,数列 满足:
满足:

 ,求数列
,求数列 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为 .且
.且 .
.(1)求数列
 的通项公式;
的通项公式;(2)若
 ,数列
,数列 满足:
满足:

 ,求数列
,求数列 的前
的前 项和
项和 .
.(1)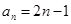 ;(2)
;(2)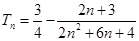 .
.
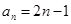 ;(2)
;(2)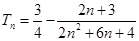 .
.试题分析:(1)根据等差数列的通项公式、求和公式把已知等式
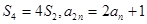 表示成首项
表示成首项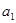 与公差
与公差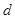 的等式, 解方程组求得首项与公差,从而得出数列
的等式, 解方程组求得首项与公差,从而得出数列 的通项公式;(2)有累加原理把
的通项公式;(2)有累加原理把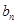 表示为
表示为 ,利用
,利用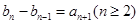 则可转化为
则可转化为 ,
, ,可用裂项相消法求出数列数列
,可用裂项相消法求出数列数列 的前
的前 项和
项和
试题解析:(1)
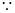
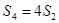 ,
,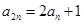 ,
,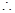
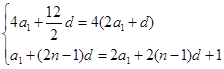 ,解得
,解得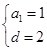 ,
,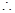
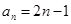 . 6分
. 6分 (2)由
 ,当
,当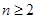 时,
时,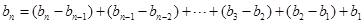
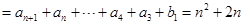 (
(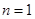 也成立).
也成立).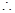
 , 9分
, 9分 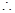
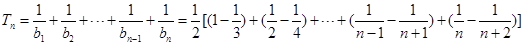
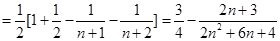 . 13分
. 13分 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
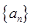 的公差
的公差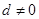 ,它的前
,它的前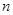 项和为
项和为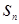 ,若
,若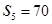 ,且
,且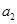 、
、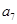 、
、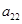 成等比数列.
成等比数列.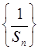 的前
的前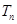 ,求证:
,求证: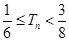 .
.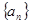 前
前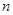 项和
项和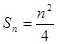 ,数列
,数列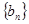 满足
满足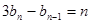 (
(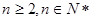 ),
),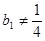 时,数列
时,数列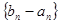 为等比数列;
为等比数列;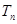 ,若数列
,若数列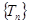 中只有
中只有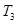 最小,求
最小,求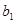 的取值范围.
的取值范围.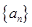 的前
的前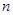 项和为
项和为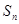 ,公差
,公差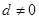 ,
,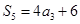 ,且
,且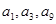 成等比数列.
成等比数列.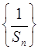 的前
的前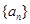 的前n项和为
的前n项和为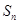 ,且满足
,且满足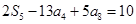 ,则下列数中恒为常数的是( )
,则下列数中恒为常数的是( )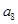
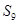
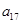
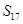
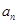 }满足a1,a3,a4成等比数列,
}满足a1,a3,a4成等比数列,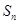 为{
为{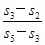 的值为( )
的值为( )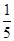
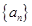 中,
中,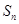 为其前n项和,若
为其前n项和,若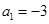 ,
,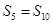 ,则当
,则当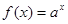 (
(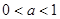 ),数列
),数列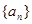 满足
满足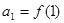 ,
,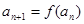 ,
,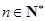 .则
.则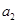 与
与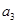 中,较大的是________;
中,较大的是________;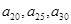 的大小关系是_____________.
的大小关系是_____________.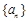 ,若点
,若点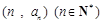 在直线
在直线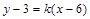 上,则数列
上,则数列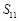 = .
= .