Question

【题目】如图，已知过点 的光线，经 轴上一点 反射后的射线 过点 .
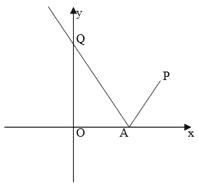
（1）求点 的坐标；
（2）若圆 过点 且与 轴相切于点 ，求圆 的方程.

Answer 1

【答案】
（1）由光线的反射角与入射角相等可知，

点 关于 轴对称点 在射线 ，

射线 所在的直线方程为 ，

即 ，令 ，则 ，

点 的坐标为 .

（2）设圆 的方程为 ，

圆 与 轴相切于点 ，

，

圆 过点 ，

，

解得 ，

圆 的方程为 .

【解析】分析：本题主要考查了直线和圆的方程的应用，解决问题的关键是（1）点 关于 轴对称点 在射线 ，所以先求入射光线所在直线的方程，然后再求与 轴的交点;（2）首先设圆的标准方程为 ，然后与 轴相切于点 得到圆心的纵坐标与半径相等，圆心的横坐标等于-1，又过点 ,代入求得圆的方程.