题目内容
函数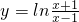 ,x∈(1,+∞)的反函数为
,x∈(1,+∞)的反函数为
- A.
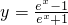 ,x∈(0,+∞)
,x∈(0,+∞) - B.
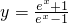 ,x∈(0,+∞)
,x∈(0,+∞) - C.
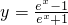 ,x∈(-∞,0)
,x∈(-∞,0) - D.
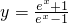 ,x∈(-∞,0)
,x∈(-∞,0)
B
分析:本题考查反函数的概念、求反函数的方法、指数式与对数式的互化,求函数的值域等函数知识和方法;
将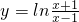 ,看做方程解出x,然后根据原函数的定义域x∈(1,+∞)求出原函数的值域,即为反函数的定义域.
,看做方程解出x,然后根据原函数的定义域x∈(1,+∞)求出原函数的值域,即为反函数的定义域.
解答:由已知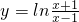 ,解x得
,解x得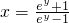 ,
,
令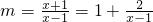 ,
,
当x∈(1,+∞)时,m∈(1,+∞),
则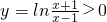 ,
,
∴函数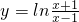 ,x∈(1,+∞)的反函数为
,x∈(1,+∞)的反函数为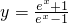 ,x∈(0,+∞)
,x∈(0,+∞)
故选B.
点评:这是一个基础性题,解题思路清晰,求解方向明确,所以容易解答;解答时注意两点,一是借助指数式和对数式的互化求x,二是函数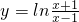 ,x∈(1,+∞)值域的确定,这里利用”常数分离法“和对数函数的性质推得.
,x∈(1,+∞)值域的确定,这里利用”常数分离法“和对数函数的性质推得.
分析:本题考查反函数的概念、求反函数的方法、指数式与对数式的互化,求函数的值域等函数知识和方法;
将
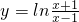 ,看做方程解出x,然后根据原函数的定义域x∈(1,+∞)求出原函数的值域,即为反函数的定义域.
,看做方程解出x,然后根据原函数的定义域x∈(1,+∞)求出原函数的值域,即为反函数的定义域.解答:由已知
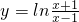 ,解x得
,解x得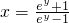 ,
,令
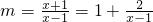 ,
,当x∈(1,+∞)时,m∈(1,+∞),
则
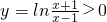 ,
,∴函数
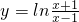 ,x∈(1,+∞)的反函数为
,x∈(1,+∞)的反函数为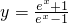 ,x∈(0,+∞)
,x∈(0,+∞)故选B.
点评:这是一个基础性题,解题思路清晰,求解方向明确,所以容易解答;解答时注意两点,一是借助指数式和对数式的互化求x,二是函数
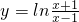 ,x∈(1,+∞)值域的确定,这里利用”常数分离法“和对数函数的性质推得.
,x∈(1,+∞)值域的确定,这里利用”常数分离法“和对数函数的性质推得. 
练习册系列答案
相关题目