题目内容
观察下列等式:
1=1 13=1
1+2=3 13+23=9
1+2+3=6 13+23+33=36
1+2+3+4=10 13+23+33+43=100
1+2+3+4+5=15 13+23+33+43+53=225
……
可以推测:13+23+33+…+n3= 。(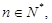 用含有n的代数式表示)
用含有n的代数式表示)
1=1 13=1
1+2=3 13+23=9
1+2+3=6 13+23+33=36
1+2+3+4=10 13+23+33+43=100
1+2+3+4+5=15 13+23+33+43+53=225
……
可以推测:13+23+33+…+n3= 。(
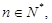 用含有n的代数式表示)
用含有n的代数式表示)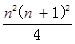
观察对比左右数列,可以发现右边是左边平方,
所以13+23+33+…+n3=(1+2+…+n)2=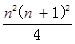
所以13+23+33+…+n3=(1+2+…+n)2=
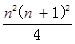

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
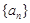 和
和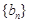 中,数列
中,数列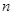 项和记为
项和记为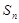 . 若点
. 若点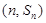 在函数
在函数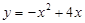 的图象上,点
的图象上,点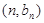 在函数
在函数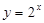 的图象上.
的图象上.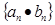 的前
的前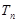
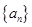 的前三项,后三数为等比数列
的前三项,后三数为等比数列 的前三项,令
的前三项,令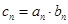 ,求数列
,求数列 的前
的前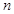 项和
项和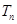 .
.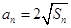 -1,
-1,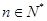 ,数列
,数列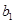 ,
,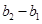 ,
,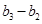 ……,
……,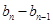 是首项为1,公比为
是首项为1,公比为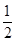 的等比数列。
的等比数列。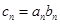 ,求数列{cn}的前n项和Tn。
,求数列{cn}的前n项和Tn。
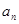 }的公差为
}的公差为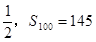 ,则
,则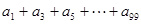 的值为 。
的值为 。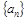 的前n项和为
的前n项和为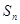 ,若
,若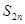 =15,则
=15,则 = .
= .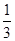 ,a2+a5=4,an=33,则n为( )
,a2+a5=4,an=33,则n为( )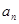 }中,
}中,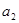 =8,前10项和S10=185.
=8,前10项和S10=185.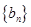 是由
是由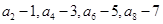 ……组成,试归纳
……组成,试归纳