题目内容
已知二次函数y=x2-6x+5.(1)求出它的图象的顶点坐标和对称轴方程;
(2)画出它的图象;
(3)分别求出它的图象和x轴、y轴的交点坐标.
分析:(1)根据二次函数的顶点坐标公式和对称轴公式分别求出即可;
(2)根据列表、描点、连线的步骤画出函数图象即可;
(3)令x=0求出对应的y值,写出坐标为与函数图象y轴的交点,令y=0求出对应的x值,写出坐标为函数图象与x轴的交点.
(2)根据列表、描点、连线的步骤画出函数图象即可;
(3)令x=0求出对应的y值,写出坐标为与函数图象y轴的交点,令y=0求出对应的x值,写出坐标为函数图象与x轴的交点.
解答: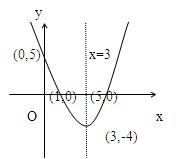 解:(1)∵a=1,b=-6,c=5
解:(1)∵a=1,b=-6,c=5
∴-
=-
=3,
=
=-4,
∴顶点坐标为(3,-4),对称轴为直线x=3.
(2)如图列表(描点略)

(3)图象与x轴相交,y=0即x2-6x+5=0解得x1=1,x2=5,所以与x轴交点的坐标为(1,0)(5,0);
图象与y轴相交,x=0解得y=5,所以与y轴交点的坐标为(0,5).
 解:(1)∵a=1,b=-6,c=5
解:(1)∵a=1,b=-6,c=5∴-
| b |
| 2a |
| -6 |
| 2 |
| 4ac-b2 |
| 4a |
| 20-36 |
| 4 |
∴顶点坐标为(3,-4),对称轴为直线x=3.
(2)如图列表(描点略)

(3)图象与x轴相交,y=0即x2-6x+5=0解得x1=1,x2=5,所以与x轴交点的坐标为(1,0)(5,0);
图象与y轴相交,x=0解得y=5,所以与y轴交点的坐标为(0,5).
点评:考查学生掌握二次函数的顶点和对称轴公式,会利用描点法画函数的图象,会求函数图象与坐标轴的交点坐标.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目