题目内容
已知三条直线a,b,c两两互相垂直,P为空间一个定点,则在过点P的直线中,分别与a,b,c所成的角都相等的直线有( )
分析:先找出:若点O是正方体ABCD-A1B1C1D1的体对角线的交点,则直线AC1、BD1、CA1、DB1分别与a,b,c所成的角都相等,进而利用平移即可找出过任意一点P的符合题意的直线.
解答:解:先说明以下结论:若点O是正方体ABCD-A1B1C1D1的体对角线的交点,则直线AC1、BD1、CA1、DB1分别与a,b,c所成的角都相等.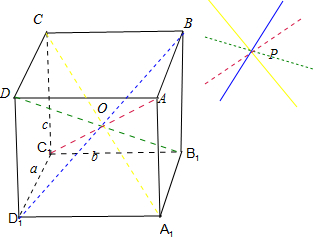
对角线AC1与直线a、b、c的夹角分别是∠AC1D1、∠AC1B1、∠AC1C,
则tan∠AC1D1=tan∠AC1B1=tan∠AC1C=
,且三个角都是锐角,故∠AC1D1=∠AC1B1=∠AC1C.
同理可得直线DB1、BD1、A1C也符合要求.
因此在过点O的直线中,分别与a,b,c所成的角都相等的直线由4条.
若点P不在点O处时,我们可以过点P分别作直线AC1、DB1、BD1、A1C的平行线,满足题意.
故选C.

对角线AC1与直线a、b、c的夹角分别是∠AC1D1、∠AC1B1、∠AC1C,
则tan∠AC1D1=tan∠AC1B1=tan∠AC1C=
| 2 |
同理可得直线DB1、BD1、A1C也符合要求.
因此在过点O的直线中,分别与a,b,c所成的角都相等的直线由4条.
若点P不在点O处时,我们可以过点P分别作直线AC1、DB1、BD1、A1C的平行线,满足题意.
故选C.
点评:把要解决的问题放在正方体里并找出容易找出适合题意的特殊点解题的关键.

练习册系列答案
相关题目