题目内容
9.如果一个几何体的三视图如图所示(单位长度:cm).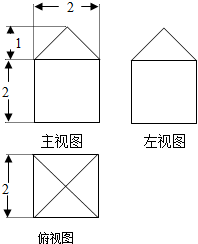
(1)求该几何体的面积S
(2)求该几何体的体积V.
分析 根据三视图可知:几何体为下面是棱长为2cm的正方体,上面是正四棱锥的组合体,
(1)求出各个面的面积,相加可得该几何体的表面积S
(2)求出正方体和棱锥的体积,相加可得该几何体的体积V.
解答 解:(1)根据三视图可知:
几何体为下面是棱长为2cm的正方体,上面是正四棱锥的组合体…(2分)
正四棱锥的底面为棱长为2cm的正方形,椎体的高为1cm,椎体的斜高为$\sqrt{2}cm$…(4分)
所以几何体的表面积为${S_{表面积}}=5×2×2+\frac{1}{2}×2×\sqrt{2}×4$=20+4$\sqrt{2}$cm2…(6分)
即表面积S=20+4$\sqrt{2}$cm2…(7分)
(2)正方体体积${V_{正方体}}={2^3}=8(c{m^3})$…(9分)
四棱锥体积${V_{四棱锥}}=\frac{1}{3}S•h=\frac{1}{3}•({2^2})•1=\frac{4}{3}(c{m^3})$…(11分)
几何体的体积$V={V_{正方体}}+V{\;}_{四棱锥}=\frac{28}{3}(c{m^3})$…(12分)
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
1.等差数列{an}的前n项和为Sn,若a2+a4+a6=18,则S7的值是( )
| A. | 21 | B. | 42 | C. | 28 | D. | 7 |