题目内容
若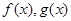 分别是R上的奇函数、偶函数,且满足
分别是R上的奇函数、偶函数,且满足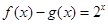 ,则有( )
,则有( )
A.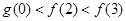 | B.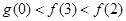 |
C.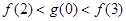 | D. |
A.
解析试题分析:因为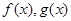 分别是R上的奇函数、偶函数.所以
分别是R上的奇函数、偶函数.所以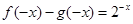 .所以
.所以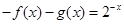 .结合已知条件可得
.结合已知条件可得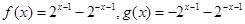 .所以
.所以 .所以选A.分别求出f(x),g(x)的解析式是关键.
.所以选A.分别求出f(x),g(x)的解析式是关键.
考点:1.函数的奇偶性.2.方程的思想.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
若函数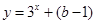 的图象不经过第二象限,则有
的图象不经过第二象限,则有
A.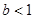 | B.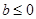 | C.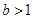 | D.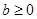 |
下列函数图象关于原点对称的有( )
①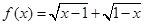 ;②
;②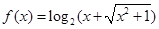 ;
;
③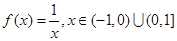 ④
④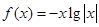 .
.
| A.①② | B.①③ | C.②③ | D.②④ |
函数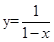 的图像与函数
的图像与函数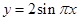 (
(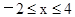 )的图像所有交点的横坐标之和等于( )
)的图像所有交点的横坐标之和等于( )
| A.2 | B.4 | C.6 | D.8 |
已知函数 ,则( )
,则( )
A.函数 的定义域为 的定义域为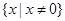 ,值域为 ,值域为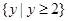 |
B.函数 的定义域为 的定义域为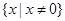 ,值域为 ,值域为 |
C.函数 的定义域为 的定义域为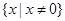 ,值域为 ,值域为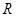 |
D.函数 的定义域为 的定义域为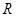 ,值域为 ,值域为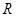 |
下列函数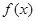 中,满足“对任意
中,满足“对任意 ,
,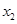
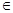 (0,
(0,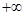 ),当
),当 <
<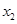 时,
时,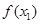 >
>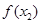 的是 ( )
的是 ( )
A.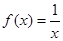 | B.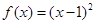 | C.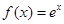 | D.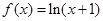 |
设定义在R上的偶函数 满足
满足 ,
,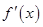 是
是 的导函数,当
的导函数,当 时,
时, ;当
;当 且
且 时,
时, .则方程
.则方程 根的个数为( )
根的个数为( )
| A.12 | B.1 6 | C.18 | D.20 |
若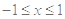 时,函数
时,函数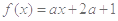 的值有正值也有负值,则
的值有正值也有负值,则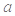 的取值范围是( )
的取值范围是( )
A.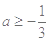 | B.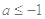 | C.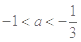 | D.以上都不对 |
已知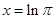 ,
,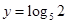 ,
,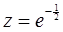 ,则
,则
A.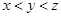 | B.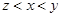 | C.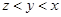 | D.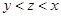 |