题目内容
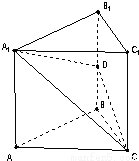 如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠B=90°,D为棱BB1上一点,且平面DA1C⊥平面AA1C1C.
如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠B=90°,D为棱BB1上一点,且平面DA1C⊥平面AA1C1C.(Ⅰ)求证:D点为棱BB1的中点;
(Ⅱ)判断四棱锥A1-B1C1CD和C-A1ABD的体积是否相等,并证明.
【答案】分析:(Ⅰ)过点D作DE⊥A1C于E点,取AC的中点F,连BF,EF,推出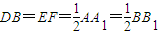 ,即可证明D点为棱BB1的中点;
,即可证明D点为棱BB1的中点;
(Ⅱ)求出四棱锥A1-B1C1CD的底面面积和高,再计算C-A1ABD的体积,即可判断体积相等.
解答:解:(1)过点D作DE⊥A1C于E点,取AC的中点F,连BF,EF.
∵面DA1C⊥面AA1C1C且相交于A1C,面DA1C内的直线DE⊥A1C,
∴DE⊥面AA1C1C.(3分)
又∵面BAC⊥面AA1C1C且相交于AC,且△ABC为等腰三角形,易知BF⊥AC,
∴BF⊥面AA1C1C.由此知:DE∥BF,从而有D,E,F,B共面,又易知BB1∥面AA1C1C,
故有DB∥EF,从而有EF∥AA1,又点F是AC的中点,
所以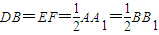 ,所以D点为棱BB1的中点.(6分)
,所以D点为棱BB1的中点.(6分)
(2)相等.ABC-A1B1C1为直三棱柱,
∴BB1⊥A1B1,BB1⊥BC,
又A1B1⊥B1C1,BC⊥AB,
∴A1B1⊥平面B1C1CD,BC⊥平面A1ABD(9分)
∴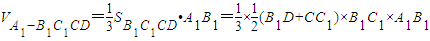
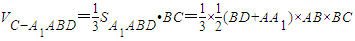
∵D为BB1中点,
∴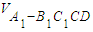 =
=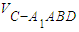 (12分)
(12分)
点评:本题考查平面与平面垂直的性质,棱柱、棱锥、棱台的体积,考查分析问题解决问题的能力,是中档题.
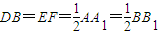 ,即可证明D点为棱BB1的中点;
,即可证明D点为棱BB1的中点;(Ⅱ)求出四棱锥A1-B1C1CD的底面面积和高,再计算C-A1ABD的体积,即可判断体积相等.
解答:解:(1)过点D作DE⊥A1C于E点,取AC的中点F,连BF,EF.
∵面DA1C⊥面AA1C1C且相交于A1C,面DA1C内的直线DE⊥A1C,
∴DE⊥面AA1C1C.(3分)
又∵面BAC⊥面AA1C1C且相交于AC,且△ABC为等腰三角形,易知BF⊥AC,
∴BF⊥面AA1C1C.由此知:DE∥BF,从而有D,E,F,B共面,又易知BB1∥面AA1C1C,
故有DB∥EF,从而有EF∥AA1,又点F是AC的中点,
所以
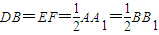 ,所以D点为棱BB1的中点.(6分)
,所以D点为棱BB1的中点.(6分)(2)相等.ABC-A1B1C1为直三棱柱,
∴BB1⊥A1B1,BB1⊥BC,
又A1B1⊥B1C1,BC⊥AB,
∴A1B1⊥平面B1C1CD,BC⊥平面A1ABD(9分)
∴
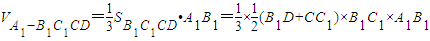
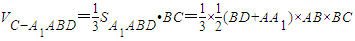
∵D为BB1中点,
∴
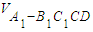 =
=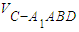 (12分)
(12分)点评:本题考查平面与平面垂直的性质,棱柱、棱锥、棱台的体积,考查分析问题解决问题的能力,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




