题目内容
在Rt△ABC中,AB=AC=1,若一个椭圆通过A、B两点,它的一个焦点为C,另一个焦点F在AB上,则这个椭圆的离心率为( )
分析:设椭圆的另一焦点为C′,依题意可求得a,进一步可求得AC′,在直角三角形ACC′中,可求得CC′,即2c,从而可求得这个椭圆的离心率.
解答:解:∵在Rt△ABC中,AB=AC=1,
∴ABC是个等腰直角三角形,
∴BC=
;
设另一焦点为C′
由椭圆定义,BC′+BC=2a,AC′+AC=2a,
设BC′=m,则AC′=1-m,
则
+m=2a,1+(1-m)=2a
两式相加得:a=
;
∴AC′=2a-AC=1+
-1=
直角三角形ACC′中,由勾股定理:(2c)2=1+
=
∴c=
.
∴e=
=
=
=
-
.
故选A.
∴ABC是个等腰直角三角形,
∴BC=
| 2 |
设另一焦点为C′
由椭圆定义,BC′+BC=2a,AC′+AC=2a,
设BC′=m,则AC′=1-m,
则
| 2 |
两式相加得:a=
2+
| ||
| 4 |
∴AC′=2a-AC=1+
| ||
| 2 |
| ||
| 2 |
直角三角形ACC′中,由勾股定理:(2c)2=1+
| 1 |
| 2 |
| 3 |
| 2 |
∴c=
| ||
| 4 |
∴e=
| c |
| a |
| ||
2+
|
(2-
| ||||
| 2 |
| 6 |
| 3 |
故选A.
点评:本题考查椭圆的简单性质,求得c=
是关键,也是难点,考查椭圆的定义与勾股定理,属于中档题.
| ||
| 4 |

练习册系列答案
相关题目
在Rt△ABC中,∠A=90°,|
|=1,则
•
的值为:( )
| AB |
| AB |
| BC |
| A、1 | B、-1 |
| C、1或-1 | D、不能确定 |
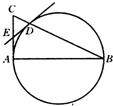 15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.
15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.