题目内容
(本小题满分6分)
已知直线 截圆心在点
截圆心在点 的圆
的圆 所得弦长为
所得弦长为 .
.
(1)求圆 的方程;
的方程;
(2)求过点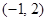 的圆
的圆 的切线方程.
的切线方程.
(1)
(2)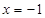 与
与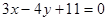
解析试题分析:(1)设圆C的半径为R , 圆心到直线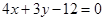 的距离为d .
的距离为d .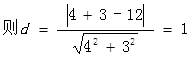 ,
,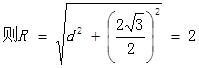
故圆C的方程为: ………………3分
………………3分
(2)当所求切线斜率不存在时,即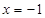 满足圆心到直线的距离为2,
满足圆心到直线的距离为2,
故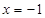 为所求的圆C的切线.…………………4分
为所求的圆C的切线.…………………4分
当切线的斜率存在时,可设方程为: 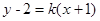 即
即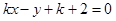
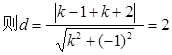 解得
解得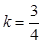 故切线为:
故切线为: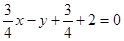
整理得: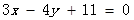
所以所求圆的切线为: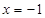 与
与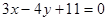 ……………6分
……………6分
考点:本题考查了圆的方程及直线与圆的位置关系
点评:在直线与圆的位置关系中,直线与圆相切时求切线、相交时求弦长是两个重点内容,要注意选择合适的方法去求解

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 是圆
是圆 上的点
上的点 的取值范围;
的取值范围; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线 交圆C于A、B两点。
交圆C于A、B两点。 时,写出直线
时,写出直线 、
、 是单位圆
是单位圆 上的点,
上的点, 是圆与
是圆与 轴正半轴的交点,三角形
轴正半轴的交点,三角形 为正三角形, 且AB∥
为正三角形, 且AB∥
 的三个三角函数值;
的三个三角函数值; 及
及 .
. 的方程为
的方程为 ,过点
,过点 作直线与圆
作直线与圆 、
、 两点。
两点。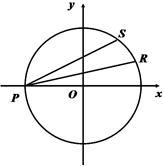
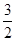 ,求直线AB的方程;
,求直线AB的方程; 的面积最大时,求直线AB的斜率;
的面积最大时,求直线AB的斜率; 作两条直线与圆O分别交于R、S,若
作两条直线与圆O分别交于R、S,若 ,且两角均为正角,试问直线RS的斜率是否为定值,并说明理由。
,且两角均为正角,试问直线RS的斜率是否为定值,并说明理由。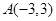 发出的光线
发出的光线 射到
射到 轴上,被
轴上,被 相切,求光线
相切,求光线 的直角三角形.过B1作直线l交椭圆于P、Q两点.
的直角三角形.过B1作直线l交椭圆于P、Q两点. ,求直线l的方程;
,求直线l的方程; ,求△B2PQ的面积
,求△B2PQ的面积 的取值范围.
的取值范围. 的端点
的端点 的坐标为
的坐标为 ,端点
,端点 在
在 :
: 上运动。
上运动。 的轨迹方程;
的轨迹方程; 与圆
与圆 ,弦
,弦 ,求直线
,求直线 为圆心的圆与直线
为圆心的圆与直线 相切.过点
相切.过点 的动直线
的动直线 与圆
与圆 相交于
相交于 ,
, 两点,
两点, 是
是 的中点,直线
的中点,直线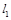 相交于点
相交于点 .
.
 时,求直线
时,求直线 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.