题目内容
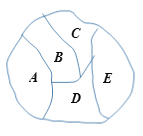
【题目】四色猜想是近代数学难题之一，四色猜想的内容是：“任何一张地图最多用四种颜色就能使具有共同边界的国家着上不同的颜色”，如图，一张地图被分成了五个区域，每个区域只使用一种颜色，现有4种颜色可供选择（四种颜色不一定用完），则满足四色猜想的不同涂色种数为__________
【答案】96
【解析】
设五个区域分别为
，其中
与
，与
，
与不相邻，根据题意，可用四种或三种颜色进行涂色，由分类加法原理和分步乘法原理，即可求解.
设五个区域分别为，
依题意由公共边的两个区域颜色不同，
用四种颜色进行涂色则有两个区域颜色相同，
可以是与，与，与同色，
有涂色方法
；
或用三种颜色涂色，则有2组颜色同色，
为与同色，与同色，有涂色方法
，
根据分类加法原理，共有涂色方法
.
故答案为：
.
练习册系列答案
相关题目
