题目内容
已知数列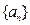 中,
中,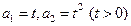 。
。
若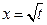 是函数
是函数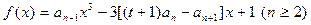 的一个极值点。
的一个极值点。
(1)求数列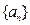 的通项公式;
的通项公式;
(2)若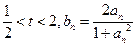 ,求证:对于任意正整数
,求证:对于任意正整数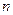 ,
,
都有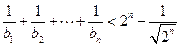 ;
;
(3)若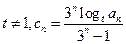 ,证明:
,证明: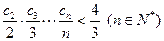
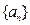 中,
中,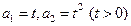 。
。若
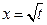 是函数
是函数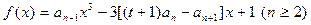 的一个极值点。
的一个极值点。(1)求数列
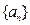 的通项公式;
的通项公式;(2)若
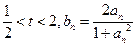 ,求证:对于任意正整数
,求证:对于任意正整数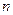 ,
,都有
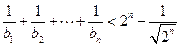 ;
;(3)若
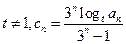 ,证明:
,证明: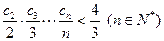
(1)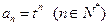 (2)(3)证明见答案
(2)(3)证明见答案
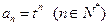 (2)(3)证明见答案
(2)(3)证明见答案(1)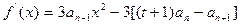 ,
,
所以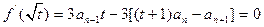 。
。
整理得: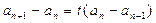 。
。
当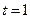 时,
时,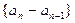 是常数列,得
是常数列,得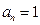 ;
;
当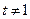 时,
时,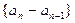 是以
是以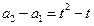 为首项,
为首项,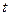 为公比的等比数列,所以
为公比的等比数列,所以
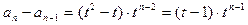
由上式得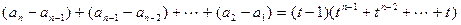 ,
,
即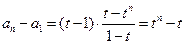 ,所以
,所以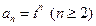 。
。
又,当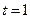 时上式仍然成立,故
时上式仍然成立,故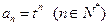 。
。
(2)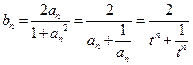 。因为
。因为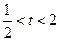 ,
,
所以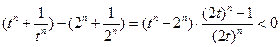 ,即
,即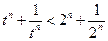 。从而
。从而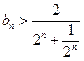 ,
,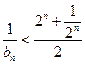 ,于是
,于是

(3)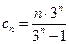 且
且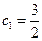 ,所以
,所以
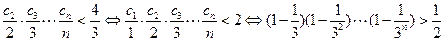
因为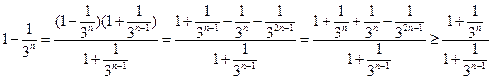 ,
,
所以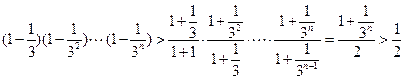 ,从而原命题得证。
,从而原命题得证。
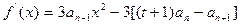 ,
,所以
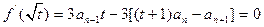 。
。整理得:
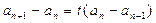 。
。当
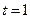 时,
时,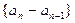 是常数列,得
是常数列,得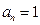 ;
;当
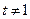 时,
时,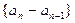 是以
是以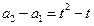 为首项,
为首项,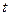 为公比的等比数列,所以
为公比的等比数列,所以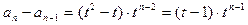
由上式得
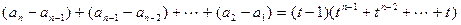 ,
,即
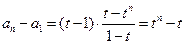 ,所以
,所以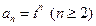 。
。又,当
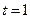 时上式仍然成立,故
时上式仍然成立,故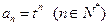 。
。(2)
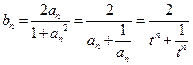 。因为
。因为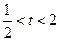 ,
,所以
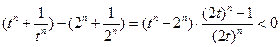 ,即
,即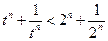 。从而
。从而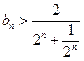 ,
,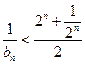 ,于是
,于是
(3)
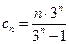 且
且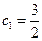 ,所以
,所以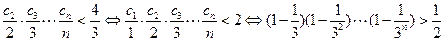
因为
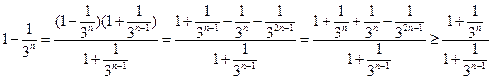 ,
,所以
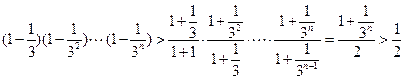 ,从而原命题得证。
,从而原命题得证。
练习册系列答案
相关题目
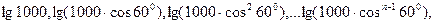 …的前多少项和为最大?
…的前多少项和为最大?
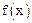 的单调区间;
的单调区间;
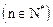 上的最小值为
上的最小值为 令
令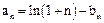 ;
;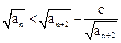 恒成立,求实数c的取值范围;
恒成立,求实数c的取值范围;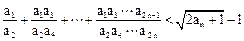 。
。 中,
中,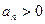 且
且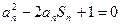 ,其中
,其中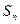 为数列
为数列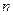 项和. (1)求证:
项和. (1)求证: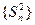 是等差数列; (2)求证:
是等差数列; (2)求证: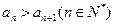 .
.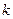 棵树种植在点
棵树种植在点 处,其中
处,其中 ,当
,当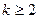 时,
时,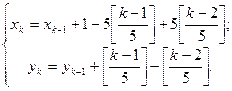 其中,
其中,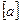 表示实数
表示实数 的整数部分,例如
的整数部分,例如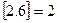 ,
,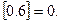 按此方案,第2008棵树种植点的坐标为 .
按此方案,第2008棵树种植点的坐标为 .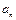 }的前n项和
}的前n项和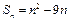 ,第k项满足5<
,第k项满足5<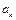 <8,则k=
<8,则k=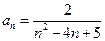 则{an}的最大项是
则{an}的最大项是
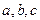 成等比数列,
成等比数列,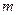 是
是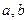 的等差中项,
的等差中项,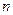 是
是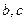 的等差中项,则
的等差中项,则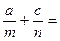 .
.