题目内容
证明以下结论:
(1)若x>y>0,则(x2-y2)(x+y)>(x2+y2)(x-y);
(2)若a>0,b>0,a≠b,则aabb>(ab)
.
(1)若x>y>0,则(x2-y2)(x+y)>(x2+y2)(x-y);
(2)若a>0,b>0,a≠b,则aabb>(ab)
| a+b | 2 |
分析:(1)对所证的不等式作差后化积,再分析乘积的符号,从而可证得结论;
(2)利用分析法,在a>0,b>0,a≠b时,要证aabb>(ab)
,需证(
)
>1;通过对a,b的大小关系的讨论,利用指数函数的性质即可使原结论得证.
(2)利用分析法,在a>0,b>0,a≠b时,要证aabb>(ab)
| a+b |
| 2 |
| a |
| b |
| a-b |
| 2 |
解答:证明:(1)∵(x2-y2)(x+y)-(x2+y2)(x-y)=(x-y)[(x+y)2-(x2+y2)]=(x-y)×2xy;
又x>y>0,
∴x-y>0,xy>0,
∴(x-y)×2xy>0,
∴(x2-y2)(x+y)>(x2+y2)(x-y);
(2)要证aabb>(ab)
,
需证aa-
•bb-
=a
•b
=(
)
>1;
∵a>0,b>0,a≠b,
∴当a>b>0时,
>1,
>0,由指数函数y=ax(a>1)的性质可知,(
)
>1;
当b>a>0时,0<
<1,
<0,由指数函数y=ax(0<a<1)的性质可知,(
)
>1;
综上所述,当a>0,b>0,a≠b时,(
)
>1成立;
故原结论成立,即a>0,b>0,a≠b,则aabb>(ab)
.
又x>y>0,
∴x-y>0,xy>0,
∴(x-y)×2xy>0,
∴(x2-y2)(x+y)>(x2+y2)(x-y);
(2)要证aabb>(ab)
| a+b |
| 2 |
需证aa-
| a+b |
| 2 |
| a+b |
| 2 |
| a-b |
| 2 |
| b-a |
| 2 |
| a |
| b |
| a-b |
| 2 |
∵a>0,b>0,a≠b,
∴当a>b>0时,
| a |
| b |
| a-b |
| 2 |
| a |
| b |
| a-b |
| 2 |
当b>a>0时,0<
| a |
| b |
| a-b |
| 2 |
| a |
| b |
| a-b |
| 2 |
综上所述,当a>0,b>0,a≠b时,(
| a |
| b |
| a-b |
| 2 |
故原结论成立,即a>0,b>0,a≠b,则aabb>(ab)
| a+b |
| 2 |
点评:本题考查综合法与分析法,着重考查转化思想推理分析、证明的能力,考查指数函数的性质,属于难题.

练习册系列答案
相关题目
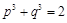 ,求证:
,求证: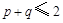 ,用反证法证明时,可假设
,用反证法证明时,可假设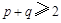 ;
;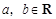 ,
,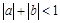 ,求证:方程
,求证:方程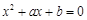 的两根的绝对值都小于1.用反证法证明时可假设方程有一根
的两根的绝对值都小于1.用反证法证明时可假设方程有一根 的绝对值大于或等于1,即假设
的绝对值大于或等于1,即假设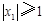 ,以下结论正确的是( )
,以下结论正确的是( )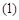 与
与 的假设都错误
的假设都错误