题目内容
三角函数内容丰富，公式很多．如果你仔细观察、敢于设想、科学求证，那么你也能发现其中的一些奥秘．请你完成以下问题：
（1）计算：（直接写答案）
+
=
+
=
（2）根据（1）的计算结果，请你猜出一个一般性的结论：
+
=
+
=
．（用数学式子加以表达，并证明你的结论，写出推理过程．）
（1）计算：（直接写答案）
| cos2° |
| sin47° |
| cos88° |
| sin133° |
| 2 |
| 2 |
| cos5° |
| sin50° |
| cos85° |
| sin130° |
| 2 |
| 2 |
（2）根据（1）的计算结果，请你猜出一个一般性的结论：
| cos(θ-45°) |
| sinθ |
| cos(135°-θ) |
| sin(180°-θ) |
| 2 |
| cos(θ-45°) |
| sinθ |
| cos(135°-θ) |
| sin(180°-θ) |
| 2 |
分析：（1）利用三角函数的诱导公式、三角函数的和角差角公式化简得：
+
=
+
=
；同理，
+
=
，
（2）根据（1）的计算结果，请你猜出一个一般性的结论：
+
=
，利用三角函数的诱导公式、三角函数的和角差角公式证明即得．
| cos2° |
| sin47° |
| cos88° |
| sin133° |
| cos2° |
| sin47° |
| sin2° |
| sin47° |
| 2 |
| cos5° |
| sin50° |
| cos85° |
| sin130° |
| 2 |
（2）根据（1）的计算结果，请你猜出一个一般性的结论：
| cos(θ-45°) |
| sinθ |
| cos(135°-θ) |
| sin(180°-θ) |
| 2 |
解答：解：（1）
+
=
+
=
=
=
同理，
+
=
，
故答案为：
；
．
（2）根据（1）的计算结果，请你猜出一个一般性的结论：
+
=
证明如下：
+
=
+
=
=
．
故答案为：（1）
，
；（2）
+
=
．
| cos2° |
| sin47° |
| cos88° |
| sin133° |
| cos2° |
| sin47° |
| sin2° |
| sin47° |
| cos2°+sin2° |
| sin47° |
| ||
| sin47° |
| 2 |
同理，
| cos5° |
| sin50° |
| cos85° |
| sin130° |
| 2 |
故答案为：
| 2 |
| 2 |
（2）根据（1）的计算结果，请你猜出一个一般性的结论：
| cos(θ-45°) |
| sinθ |
| cos(135°-θ) |
| sin(180°-θ) |
| 2 |
证明如下：
| cos(θ-45°) |
| sinθ |
| cos(135°-θ) |
| sin(180°-θ) |
| cos(θ-45°) |
| sinθ |
| sin(θ-45°) |
| sinθ |
| ||
| sinθ |
| 2 |
故答案为：（1）
| 2 |
| 2 |
| cos(θ-45°) |
| sinθ |
| cos(135°-θ) |
| sin(180°-θ) |
| 2 |
点评：本小题主要考查三角函数的诱导公式、三角函数的和角差角公式、类比推理等基础知识，考查运算求解能力，考查化归与转化思想．属于基础题．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
在某次试验中，有两个试验数据x，y，统计的结果如下面的表格
=______
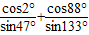