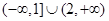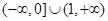题目内容
定义在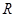 上的函数
上的函数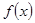 满足
满足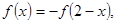 且当
且当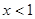 时
时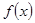 递增, 若
递增, 若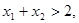
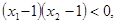 则
则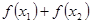 的值是 ( )
的值是 ( )
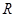 上的函数
上的函数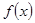 满足
满足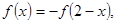 且当
且当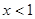 时
时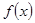 递增, 若
递增, 若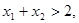
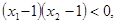 则
则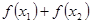 的值是 ( )
的值是 ( ) | A.恒为正数 | B.恒为负数 | C.等于0 | D.正、负都有可能 |
A
试题分析:利用已知等式得到f(x)关于(1,0)对称,由
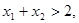 ,
,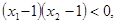 知两数一个大于1一个小于1,且大于1的离对称中心远,利用单调性得到函数值的大小.
知两数一个大于1一个小于1,且大于1的离对称中心远,利用单调性得到函数值的大小.∵
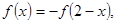 ,∴f(x)关于(1,0)对称
,∴f(x)关于(1,0)对称∵当x<1时f(x)递增∴f(x)在R上递增
∵
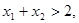 ,
,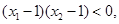 ,∴
,∴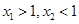 且
且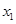 离(1,0)远
离(1,0)远∴
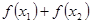 >0
>0故选A
点评:本题考查抽象函数的性质、利用函数的单调性判断函数值的正负.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
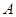 、
、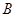 两个项目,预计投资
两个项目,预计投资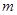 万元可获得利润
万元可获得利润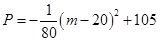
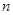 万元可获得利润
万元可获得利润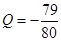
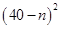
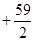
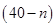 万元.若该企业用40
万元.若该企业用40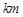 的A,B两家工厂(视作污染源)的污染强度分别为
的A,B两家工厂(视作污染源)的污染强度分别为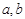 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数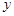 等于两家工厂对该处的污染指数之和.设
等于两家工厂对该处的污染指数之和.设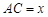 (
(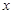 的函数;
的函数;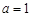 ,且
,且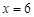 时,
时,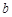 的值.
的值.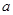 元(一年定期),若年利率为
元(一年定期),若年利率为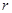 保持不变,且每年到期存款和利息自动转为新的一年定期,到2012年底将所有存款及利息全部取回,则可取回的钱数(元)为
保持不变,且每年到期存款和利息自动转为新的一年定期,到2012年底将所有存款及利息全部取回,则可取回的钱数(元)为

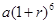
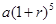
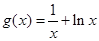 ,
,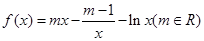 .
.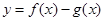 在
在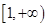 上为单调函数,求m的取值范围;
上为单调函数,求m的取值范围;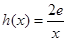 ,若在
,若在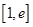 上至少存在一个
上至少存在一个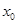 ,使得
,使得 成立,求
成立,求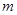 的取值范围.
的取值范围.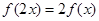 的是( )
的是( )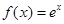
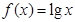
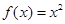
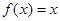
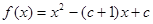
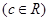 .
.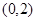 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;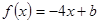 ,且不等式
,且不等式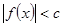 的解集为
的解集为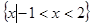 ,
,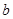 的值;
的值; 的不等式
的不等式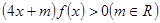
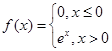 ,则使函数g(x)=f(x)+x-m有零点的实数m的取值范围是
,则使函数g(x)=f(x)+x-m有零点的实数m的取值范围是