题目内容
已知:平面α∩平面β=直线a.α,β同垂直于平面γ,又同平行于直线b.求证:(1)a⊥γ;(2)b⊥γ.

【答案】分析:(1)在γ内任取一点P并于γ内作直线PM⊥AB,PN⊥AC,由面面垂直的性质得PM⊥α,PM⊥a; 同理证明PN⊥a,这样a垂直于面γ内的2条相交直线,从而a⊥γ.
(2)通过α,β同垂直于平面γ,又同平行于直线b,利用线面平行的性质定理证明,b∥a,由(1)知a⊥γ,从而证得b⊥γ.
解答: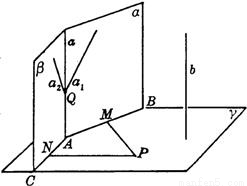 证明:(1)设α∩γ=AB,β∩γ=AC.
证明:(1)设α∩γ=AB,β∩γ=AC.
在γ内任取一点P并于γ内作直线PM⊥AB,PN⊥AC.
∵γ⊥α,
∴PM⊥α.
而a?α,
∴PM⊥a.
同理PN⊥a.又PM?γ,PN?γ,
∴a⊥γ.
(2)于a上任取点Q,过b与Q作一平面交α于直线a1,交β于直线a2.∵b∥α,∴b∥a1.
同理b∥a2.∵a1,a2同过Q且平行于b,
∵a1,a2重合.
又a1?α,a2?β,
∴a1,a2都是α、β的交线,即都重合于a.∵b∥a1,∴b∥a.
而a⊥γ,
∴b⊥γ.
点评:本题考查证明线面垂直的证明方法.
(2)通过α,β同垂直于平面γ,又同平行于直线b,利用线面平行的性质定理证明,b∥a,由(1)知a⊥γ,从而证得b⊥γ.
解答:
 证明:(1)设α∩γ=AB,β∩γ=AC.
证明:(1)设α∩γ=AB,β∩γ=AC.在γ内任取一点P并于γ内作直线PM⊥AB,PN⊥AC.
∵γ⊥α,
∴PM⊥α.
而a?α,
∴PM⊥a.
同理PN⊥a.又PM?γ,PN?γ,
∴a⊥γ.
(2)于a上任取点Q,过b与Q作一平面交α于直线a1,交β于直线a2.∵b∥α,∴b∥a1.
同理b∥a2.∵a1,a2同过Q且平行于b,
∵a1,a2重合.
又a1?α,a2?β,
∴a1,a2都是α、β的交线,即都重合于a.∵b∥a1,∴b∥a.
而a⊥γ,
∴b⊥γ.
点评:本题考查证明线面垂直的证明方法.

练习册系列答案
相关题目
 已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等腰直角三角形,AC⊥AD,且AD=DE=2AB,F为CD中点.
已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等腰直角三角形,AC⊥AD,且AD=DE=2AB,F为CD中点. ,如图所示.
,如图所示.
 ,如图所示.
,如图所示.