题目内容
已知数列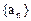 满足
满足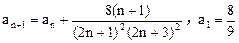 ,求数列
,求数列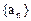 的通项公式。
的通项公式。
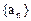 满足
满足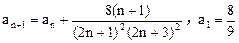 ,求数列
,求数列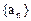 的通项公式。
的通项公式。解:由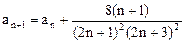 及
及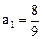 ,得
,得
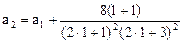
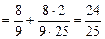
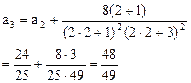
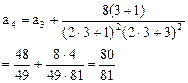
由此可猜测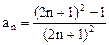 ,往下用数学归纳法证明这个结论。
,往下用数学归纳法证明这个结论。
(1)当n=1时,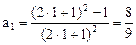 ,所以等式成立。
,所以等式成立。
(2)假设当n=k时等式成立,即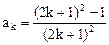 ,则当
,则当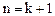 时,
时,
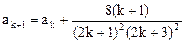
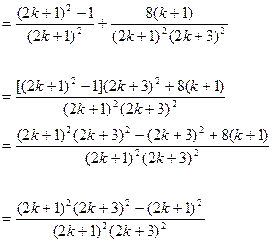
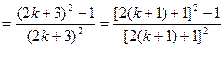
由此可知,当n=k+1时等式也成立。
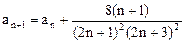 及
及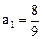 ,得
,得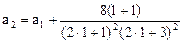
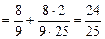
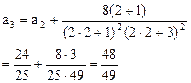
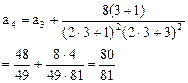
由此可猜测
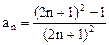 ,往下用数学归纳法证明这个结论。
,往下用数学归纳法证明这个结论。(1)当n=1时,
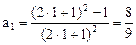 ,所以等式成立。
,所以等式成立。(2)假设当n=k时等式成立,即
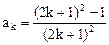 ,则当
,则当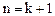 时,
时,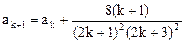
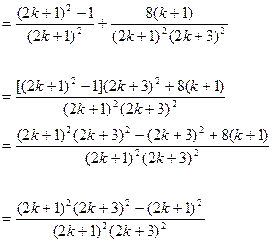
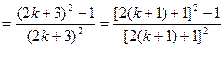
由此可知,当n=k+1时等式也成立。
根据(1)(2)可知,等式对任何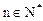
评注:本题解题的关键是通过首项和递推关系式先求出数列的前n项,进而猜出数列的通项公式,最后再用数学归纳法加以证明。
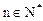
评注:本题解题的关键是通过首项和递推关系式先求出数列的前n项,进而猜出数列的通项公式,最后再用数学归纳法加以证明。

练习册系列答案
相关题目
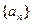 的前
的前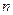 项和为
项和为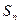 ,已知
,已知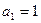 ,
,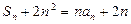 (
(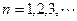 ).(Ⅰ)求证:数列
).(Ⅰ)求证:数列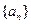 为等差数列,并分别写出
为等差数列,并分别写出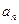 和
和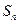 关于
关于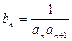 ,
,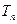 为数列
为数列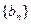 前
前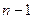 项和,求
项和,求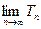 ;(Ⅲ)是否存在自然数
;(Ⅲ)是否存在自然数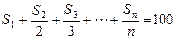 ? 若存在,求
? 若存在,求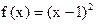 ,
,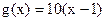 ,数列
,数列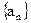 满足
满足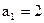 ,
,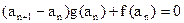 ,
,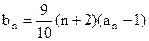 .
.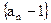 是等比数列;
是等比数列;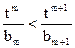 对任意
对任意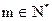 恒成立,求实数
恒成立,求实数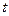 的取值范围.
的取值范围.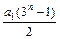 (对于所有n≥1),且a4=54,则a1的数值是_____.
(对于所有n≥1),且a4=54,则a1的数值是_____.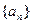 的前n项和为Sn,点
的前n项和为Sn,点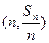 的直线
的直线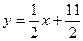 上,数列
上,数列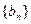 满足
满足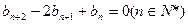 ,
,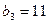 ,且
,且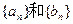 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设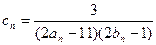 ,记数列
,记数列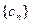 的前n项和为Tn,求使不等式
的前n项和为Tn,求使不等式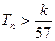 对一切
对一切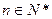 都成立的最大正整数k的值.
都成立的最大正整数k的值.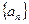 中,
中,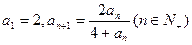 ,求数列
,求数列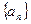 中,
中, 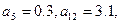 求
求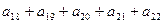 的值
的值
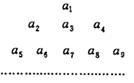
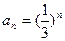 ,把数列{an}的各项排成如右图所示三角形形状,记
,把数列{an}的各项排成如右图所示三角形形状,记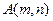 表示第m行、第n列的项,则
表示第m行、第n列的项,则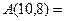 ,
,