题目内容
2.设函数f(x)=ln(1+x),g(x)=xf′(x)(x≥0),其中f′(x)是f(x)的导函数.(1)若a≤1,求证:f(x)≥ag(x).
(2)若g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N+,求g1(x),g2(x),g3(x)解析式,猜想gn(x)的解析式,并用数学归纳法证明.
分析 (1)f(x)=ln(1+x),可得f′(x)=$\frac{1}{1+x}$.(x≥0).g(x)=$\frac{x}{1+x}$.f(x)≥ag(x)即ln(1+x)≥$\frac{ax}{1+x}$?(1+x)ln(1+x)-ax≥0.令h(x)=(1+x)ln(1+x)-ax(x≥0).
利用导数研究其单调性即可得出.
(2)g1(x)=g(x)=$\frac{x}{1+x}$,利用gn+1(x)=g(gn(x)),n∈N+,可得g2(x)=g(g1(x))=$\frac{x}{1+2x}$.g3(x)=g(g2(x))=$\frac{x}{1+3x}$,猜想:gn(x)=$\frac{x}{1+nx}$.利用数学归纳法证明即可.
解答 (1)证明:∵f(x)=ln(1+x),∴f′(x)=$\frac{1}{1+x}$.(x≥0).
∴g(x)=$\frac{x}{1+x}$.f(x)≥ag(x)即ln(1+x)≥$\frac{ax}{1+x}$?(1+x)ln(1+x)-ax≥0.
令h(x)=(1+x)ln(1+x)-ax(x≥0).
h′(x)=ln(1+x)+1-a,
∵a≤1,∴1-a≥0,
又x≥0,ln(1+x)≥0,
∴h′(x)=ln(1+x)+1-a≥0,
∴h(x)在x≥0时单调递增,又h(0)=0,
∴h(x)≥0,即ln(1+x)≥$\frac{ax}{1+x}$,
∴f(x)≥ag(x).
(2)解:g1(x)=g(x)=$\frac{x}{1+x}$,
∵gn+1(x)=g(gn(x)),n∈N+,
∴g2(x)=g(g1(x))=$g(\frac{x}{1+x})$=$\frac{\frac{x}{1+x}}{1+\frac{x}{1+x}}$=$\frac{x}{1+2x}$.
g3(x)=g(g2(x))=$g(\frac{x}{1+2x})$=$\frac{\frac{x}{1+2x}}{1+\frac{x}{1+2x}}$=$\frac{x}{1+3x}$,
猜想:gn(x)=$\frac{x}{1+nx}$.
下面利用数学归纳法证明:
①当n=1时,g1(x)=g(x)=$\frac{x}{1+x}$,成立.
②假设当n=k(k∈N*)时,gk(x)=$\frac{x}{1+kx}$.
则当n=k+1时,gk+1(x)=g(gk(x))=$g(\frac{x}{1+kx})$=$\frac{\frac{x}{1+kx}}{1+\frac{x}{1+kx}}$=$\frac{x}{1+(k+1)x}$,
因此当n=k+1时,gn(x)=$\frac{x}{1+nx}$也成立.
综上可得:?n∈N*,gn(x)=$\frac{x}{1+nx}$成立.
点评 本题考查了利用数学归纳法证明等式的方法、利用导数研究函数的单调性证明不等式的方法,考查了猜想能力、推理能力与计算能力,属于中档题.

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 与
与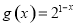 在同一直角坐标系下的图象大致是( )
在同一直角坐标系下的图象大致是( )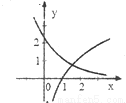 B.
B.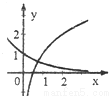
 D.
D.