题目内容
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4.设圆C的半径为1,圆心在l上.
(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使|MA|=2|MO|,求圆心C的横坐标a的取值范围.
(1) y=3或3x+4y-12=0 (2)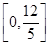
解析解 (1)由题设,圆心C是直线y=2x-4和y=x-1的交点,解得点C(3,2),于是切线的斜率必存在.
设过A(0,3)的圆C的切线方程为y=kx+3,由题意,得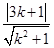 =1,解得k=0或-
=1,解得k=0或-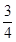 ,故所求切线方程为y=3或3x+4y-12=0.
,故所求切线方程为y=3或3x+4y-12=0.
(2)因为圆心在直线y=2x-4上,
所以圆C的方程为(x-a)2+[y-2(a-2)]2=1.
设点M(x,y),因为|MA|=2|MO|,所以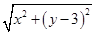 =2
=2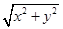 ,化简得x2+y2+2y-3=0,即x2+(y+1)2=4,所以点M在以D(0,-1)为圆心,2为半径的圆上.
,化简得x2+y2+2y-3=0,即x2+(y+1)2=4,所以点M在以D(0,-1)为圆心,2为半径的圆上.
由题意,点M(x,y)在圆C上,所以圆C与圆D有公共点,则|2-1|≤|CD|≤2+1,
即1≤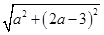 ≤3.整理得-8≤5a2-12a≤0.
≤3.整理得-8≤5a2-12a≤0.
由5a2-12a+8≥0,得a∈R;由5a2-12a≤0,得0≤a≤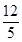 .
.
所以点C的横坐标a的取值范围是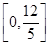 .
.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 是否相切?说明理由.
是否相切?说明理由.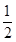 .
. 经过点
经过点 和
和
 上,求圆
上,求圆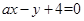 与圆
与圆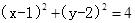 。
。 ,求a的值。
,求a的值。