题目内容
三个实数成等差数列,其首项是9.若将其第二项加2、第三项加20,则这三个数依次构成等比数列{an},那么a3的所有可能取值中最小的是( )
| A、1 | B、4 | C、36 | D、49 |
分析:设出等差数列的3项,结合其第二项加2、第三项加20,得到的三个数依次构成等比数列列式求得d的值,则
a3的最小取值可求.
a3的最小取值可求.
解答:解:设三数分别为9,9+d,9+2d,
∵其第二项加2、第三项加20,得到的三个数依次构成等比数列,
∴(9+d+2)2=9(9+2d+20),
整理,得(d+11)2=9(2d+29),
d2+4d-140=0,
(d+14)(d-10)=0.
解得:d=-14或d=10.
当d=-14时,a3=9+2d+20=9-28+20=1;
d=10时,a3=9+20+20=49.
∴a3的取值最小是1.
故选:A.
∵其第二项加2、第三项加20,得到的三个数依次构成等比数列,
∴(9+d+2)2=9(9+2d+20),
整理,得(d+11)2=9(2d+29),
d2+4d-140=0,
(d+14)(d-10)=0.
解得:d=-14或d=10.
当d=-14时,a3=9+2d+20=9-28+20=1;
d=10时,a3=9+20+20=49.
∴a3的取值最小是1.
故选:A.
点评:本题考查了等差数列的性质,考查了等比中项的概念,训练了分类讨论的数学思想方法,属中档题.

练习册系列答案
相关题目
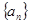 ,则
,则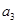 的所有取值中的最小值是( )
的所有取值中的最小值是( )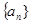 ,那么
,那么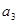 的所有可能取值中最小的是( )
的所有可能取值中最小的是( )