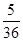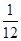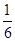题目内容
在正四面体的6条棱中随机抽取2条,则其2条棱互相垂直的概率为( )
A. | B. | C. | D. |
C
解析试题分析:根据题意,如图,在正四面体A-BCD的6条棱中随机抽取2条,有C62=15种情况,
又由正四面体的几何结构,其中相互垂直的棱有AC、BD,AB、CD,AD、BC,共3组,
则其概率P=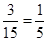 ,故选C.
,故选C.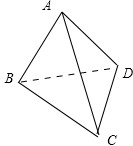
考点:本题主要考查古典概型概率的计算。
点评:小综合题,结合正四面体,确定相互垂直的棱的数目是解题的关键。

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
从三件正品、一件次品中随机取出两件,则取出的产品全是正品的概率是
A. | B. | C.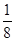 | D.无法确定 |
某产品分甲、乙、丙三级,其中乙、丙两级均属次品,在正常生产情况下,出现乙级品和丙级品的概率分别是5%和3%,则抽验一只是正品(甲级)的概率为( )
| A.0.95 | B.0.97 | C.0.92 | D.0.08 |
从装有 个红球和
个红球和 个黒球的口袋内任取
个黒球的口袋内任取 个球,那么互斥而不对立的两个事件是
个球,那么互斥而不对立的两个事件是
| A.至少有一个黒球与都是红球 | B.至少有一个黒球与都是黒球 |
C.至少有一个黒球与至少有 个红球 个红球 | D.恰有 个黒球与恰有 个黒球与恰有 个黒球 个黒球 |
设随机变量X~ ,则P(X=3)的值是( )
,则P(X=3)的值是( )
A. | B. | C. | D. |
已知ξ~N(0,62),且P(-2≤ξ≤0)=0.4,则P(ξ>2)等于( )
| A.0.1 | B.0.2 | C.0.6 | D.0.8 |
 米的绳子,拉直后在任意位置剪断,则剪得两段的长度都不小于1米,且以剪得的两段绳为两边的矩形的面积都不大于
米的绳子,拉直后在任意位置剪断,则剪得两段的长度都不小于1米,且以剪得的两段绳为两边的矩形的面积都不大于 平方米的概率为( )
平方米的概率为( )



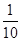
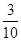
 为( )
为( )