题目内容
(文)设F1、F2分别为椭圆C: (m>0,n>0且m≠n)的两个焦点.
(m>0,n>0且m≠n)的两个焦点.(1)若椭圆C上的点A(1,
 )到两个焦点的距离之和等于4,求椭圆C的方程.
)到两个焦点的距离之和等于4,求椭圆C的方程.(2)如果点P是(1)中所得椭圆上的任意一点,且
 ,求△PF1F2的面积.
,求△PF1F2的面积.(3)若椭圆C具有如下性质:设M、N是椭圆C上关于原点对称的两点,点Q是椭圆上任意一点,且直线QM与直线QN的斜率都存在,分别记为KQM、KQN,那么KQM和KQN之积是与点Q位置无关的定值.试问:双曲线
 (a>0,b>0)是否具有类似的性质?并证明你的结论.通过对上面问题进一步研究,请你概括具有上述性质的二次曲线更为一般的结论,并说明理由.
(a>0,b>0)是否具有类似的性质?并证明你的结论.通过对上面问题进一步研究,请你概括具有上述性质的二次曲线更为一般的结论,并说明理由.
【答案】分析:(1)利用椭圆定义先求m=,再根据点A(1, )在椭圆上求n的值,需要主要进行分类讨论
)在椭圆上求n的值,需要主要进行分类讨论
(2)利用椭圆定义得 PF1+PF2=2m,PF12+PF22=4,从而有 PF1PF2=6,故可求△PF1F2的面积;
(3)设M,N是双曲线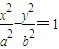 (a>0,b>0)上关于原点对称的两点,点Q是椭圆上任意一点,且直线QM与直线QN的斜率都存在,利用点差法可证
(a>0,b>0)上关于原点对称的两点,点Q是椭圆上任意一点,且直线QM与直线QN的斜率都存在,利用点差法可证
解答:解:(1)当m>n时,由椭圆定义得 2m=4,∴m=2(2分)
又点A(1, )在椭圆上 所以
)在椭圆上 所以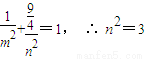
∴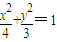 (3分)
(3分)
同理,当m<n时,椭圆方程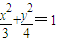 (4分)
(4分)
(2)当m>n时,由椭圆定义得 PF1+PF2=2m,PF12+PF22=4
解得 PF1PF2=6 (8分)
所以△PF1F2的面积为3
同理,当m<n时,△PF1F2的面积也为3 (10分)
(3)设M,N是双曲线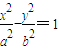 (a>0,b>0)上关于原点对称的两点,点Q是椭圆上任意一点,且直线QM与直线QN的斜率都存在,分别记为KQM,KQN,那么KQM,KQN之积是与点Q位置无关的定值.
(a>0,b>0)上关于原点对称的两点,点Q是椭圆上任意一点,且直线QM与直线QN的斜率都存在,分别记为KQM,KQN,那么KQM,KQN之积是与点Q位置无关的定值.
设点M(x1,y1),N(-x1,-y1).Q(x,y)
则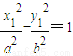 ,
,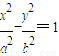
作差得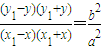 (12分)
(12分)
所以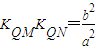 (14分)
(14分)
设M,N是二次曲线mx2+ny2=1上关于原点对称的两点,点Q是二次曲线上任意一点,且直线QM与直线QN的斜率都存在,分别记为KQM,KQN,
那么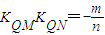 (15分)
(15分)
证明 设点点M(x1,y1),N(-x1,-y1).Q(x,y)
则mx12+ny12=1,mx2+ny2=1
作差得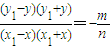 ∴
∴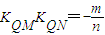 (18分)
(18分)
点评:本题的考点是椭圆的定义,主要考查椭圆的定义,考查三角形的面积,考查点差法求解斜率问题,综合性较强.
 )在椭圆上求n的值,需要主要进行分类讨论
)在椭圆上求n的值,需要主要进行分类讨论(2)利用椭圆定义得 PF1+PF2=2m,PF12+PF22=4,从而有 PF1PF2=6,故可求△PF1F2的面积;
(3)设M,N是双曲线
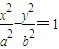 (a>0,b>0)上关于原点对称的两点,点Q是椭圆上任意一点,且直线QM与直线QN的斜率都存在,利用点差法可证
(a>0,b>0)上关于原点对称的两点,点Q是椭圆上任意一点,且直线QM与直线QN的斜率都存在,利用点差法可证解答:解:(1)当m>n时,由椭圆定义得 2m=4,∴m=2(2分)
又点A(1,
 )在椭圆上 所以
)在椭圆上 所以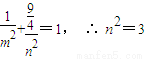
∴
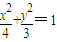 (3分)
(3分)同理,当m<n时,椭圆方程
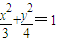 (4分)
(4分)(2)当m>n时,由椭圆定义得 PF1+PF2=2m,PF12+PF22=4
解得 PF1PF2=6 (8分)
所以△PF1F2的面积为3
同理,当m<n时,△PF1F2的面积也为3 (10分)
(3)设M,N是双曲线
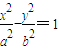 (a>0,b>0)上关于原点对称的两点,点Q是椭圆上任意一点,且直线QM与直线QN的斜率都存在,分别记为KQM,KQN,那么KQM,KQN之积是与点Q位置无关的定值.
(a>0,b>0)上关于原点对称的两点,点Q是椭圆上任意一点,且直线QM与直线QN的斜率都存在,分别记为KQM,KQN,那么KQM,KQN之积是与点Q位置无关的定值.设点M(x1,y1),N(-x1,-y1).Q(x,y)
则
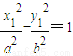 ,
,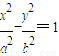
作差得
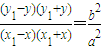 (12分)
(12分)所以
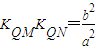 (14分)
(14分)设M,N是二次曲线mx2+ny2=1上关于原点对称的两点,点Q是二次曲线上任意一点,且直线QM与直线QN的斜率都存在,分别记为KQM,KQN,
那么
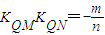 (15分)
(15分)证明 设点点M(x1,y1),N(-x1,-y1).Q(x,y)
则mx12+ny12=1,mx2+ny2=1
作差得
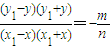 ∴
∴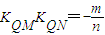 (18分)
(18分)点评:本题的考点是椭圆的定义,主要考查椭圆的定义,考查三角形的面积,考查点差法求解斜率问题,综合性较强.

练习册系列答案
相关题目
 上一点,双曲线的一条渐近线方程为3x-2y=0,F1、F2分别是双曲线左右焦点.若|PF1|=5,则|PF2|=( )
上一点,双曲线的一条渐近线方程为3x-2y=0,F1、F2分别是双曲线左右焦点.若|PF1|=5,则|PF2|=( ) 上一点,双曲线的一条渐近线方程为3x-2y=0,F1、F2分别是双曲线左右焦点.若|PF1|=5,则|PF2|=( )
上一点,双曲线的一条渐近线方程为3x-2y=0,F1、F2分别是双曲线左右焦点.若|PF1|=5,则|PF2|=( ) 上一点,双曲线的一条渐近线方程为3x-2y=0,F1、F2分别是双曲线左右焦点.若|PF1|=5,则|PF2|=( )
上一点,双曲线的一条渐近线方程为3x-2y=0,F1、F2分别是双曲线左右焦点.若|PF1|=5,则|PF2|=( )