题目内容
【题目】如图,在四棱锥P-ABCD中,平面PAD⊥底面 ABCD,侧棱PA=PD=![]() ,底面ABCD为直角梯形,其中BC∥AD ,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD ,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
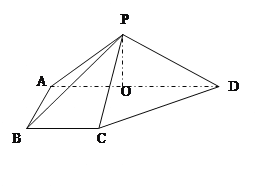
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)线段AD上是否存在点![]() ,使得它到平面PCD的距离为
,使得它到平面PCD的距离为![]() ?若存在,求出
?若存在,求出![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
试题(Ⅰ)只需证明![]() ,又由面面垂直的性质定理知
,又由面面垂直的性质定理知![]() 平面
平面![]() ;
;
(Ⅱ)连接![]() 、
、![]() ,假设存在点
,假设存在点![]() ,使得它到平面
,使得它到平面![]() 的距离为
的距离为![]() ,设
,设![]() ,由
,由![]() ,求得
,求得![]() 的值即可.
的值即可.
试题解析:(Ⅰ)证明:在![]() 中
中![]() ,
,![]() 为
为![]() 中点,所以
中点,所以![]() .
.
又侧面![]() 底面
底面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)连接![]() 、
、![]()
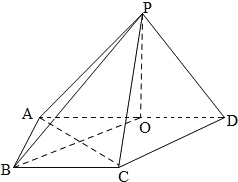
假设存在点![]() ,使得它到平面
,使得它到平面![]() 的距离为
的距离为![]() .
.
设![]() ,则
,则![]()
因为![]() ,
,![]() 为
为![]() 的中点,
的中点,![]()
所以![]() ,且
,且![]()
所以![]()
因为![]() ,且
,且![]()
所以![]()
在![]() 中,
中,![]()
所以![]()
所以![]()
由![]() ,即
,即![]()
解得![]()
所以存在点![]() 满足题意,此时
满足题意,此时![]() .
.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
【题目】中国的钨矿资源储量丰富,在全球已经探明的钨矿产资源储量中占比近![]() ,居全球首位。中国又属赣州钨矿资源最为丰富,其素有“世界钨都”之称。某科研单位在研发的钨合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值与这种新合金材料的含量x(单位:克)的关系为:当
,居全球首位。中国又属赣州钨矿资源最为丰富,其素有“世界钨都”之称。某科研单位在研发的钨合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值与这种新合金材料的含量x(单位:克)的关系为:当![]() 时,
时, ![]() 是
是![]() 的二次函数;当
的二次函数;当![]() 时,
时, ![]() .测得部分数据如表.
.测得部分数据如表.
x(单位:克) | 0 | 1 | 2 | 9 | … |
y | 0 |
| 3 |
| … |
(1)求y关于x的函数关系式y=![]()
(2)求函数![]() 的最大值
的最大值





