题目内容
(本小题12分)如图为等腰直角三角形直角边长为8,![]() ,
,![]() ,沿DE将三角形ADE折起使得点A在平面BCED上的射影是点C, MC=
,沿DE将三角形ADE折起使得点A在平面BCED上的射影是点C, MC=![]() AC.
AC.
(Ⅰ)在BD上确定点N的位置,使得![]() ;
;
 (Ⅱ)求CN与平面ABD所成角的正弦值.
(Ⅱ)求CN与平面ABD所成角的正弦值.
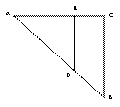
(本小题12分)(Ⅰ)解析:由已知, 点A在平面BCED上的射影是点C,
则可知![]() ,而
,而![]() 如图建立空间直
如图建立空间直
角坐标系,则可知各点的坐标为
C(0,0,0),A(0,0,4),B(0,8,0),D(3,5,0),E(3,0,0)----------------------- 2分
 由MC=
由MC=![]() AC,可知点M的坐标为(0,0,
AC,可知点M的坐标为(0,0,![]() ),设点N 的坐标为(x,y,0)
),设点N 的坐标为(x,y,0)
则可知y=8-x,即点N 的坐标为(x,8-x,0)
设平面ADE的法向量为![]() ,
,
由题意可知![]() ,而
,而![]() ,
,![]()
可得![]() ,取x=4,则z=3,
,取x=4,则z=3,
可得![]() ----------------------------------------------------------4分
----------------------------------------------------------4分
要使![]() 等价于
等价于![]() 即
即![]()
解之可得![]() ,即可知点N的坐标为(2,6,0),点N为BD的三等分点.------6分
,即可知点N的坐标为(2,6,0),点N为BD的三等分点.------6分
(Ⅱ)由(Ⅰ)可知![]() ,设平面ADB的法向量为
,设平面ADB的法向量为![]() ,由题意可知
,由题意可知
![]() ,而
,而![]() ,
,![]() 可得
可得![]() ,取x=1,则y=1,z=2
,取x=1,则y=1,z=2
可得![]() ------------------------------------------------10分
------------------------------------------------10分
设CN与平面ABD所成角为![]() ,
, =
=![]() ---------------12分
---------------12分

练习册系列答案
相关题目
 中,AC=BC, AC⊥BC,点D是A1B1中点.
中,AC=BC, AC⊥BC,点D是A1B1中点.  ,求二面角D- AC1-A1的余弦值.
,求二面角D- AC1-A1的余弦值.
 中,
中, 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是 的菱形,
的菱形, 为
为 的中点.
的中点. 与底面
与底面 平面
平面 ;
; 的余弦值.
的余弦值. 
 中,底面
中,底面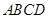 是正方形,
是正方形, ,
,  底面
底面 分别在
分别在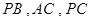 上,且
上,且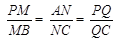
 ∥平面
∥平面 .
. 与平面面
与平面面

 平面BCD;
平面BCD;