题目内容
(本题满分12分)
已知函数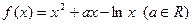 .
.
(I)若函数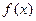 在
在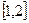 上是减函数,求实数
上是减函数,求实数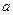 的取值范围;
的取值范围;
(II)令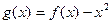 ,是否存在实数
,是否存在实数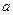 ,使得当
,使得当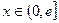 时,函数
时,函数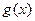 的最小值是
的最小值是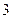 ,若存在,求出实数
,若存在,求出实数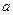 的值,若不存在,说明理由?
的值,若不存在,说明理由?
(III)当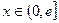 时,证明:
时,证明: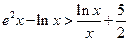 .
.
已知函数
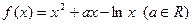 .
.(I)若函数
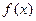 在
在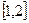 上是减函数,求实数
上是减函数,求实数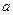 的取值范围;
的取值范围;(II)令
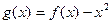 ,是否存在实数
,是否存在实数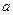 ,使得当
,使得当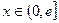 时,函数
时,函数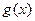 的最小值是
的最小值是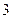 ,若存在,求出实数
,若存在,求出实数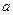 的值,若不存在,说明理由?
的值,若不存在,说明理由?(III)当
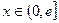 时,证明:
时,证明: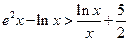 .
.(I)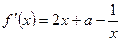 …………………………………1分
…………………………………1分
 在
在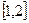 上单调递减,因此当
上单调递减,因此当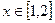
 时,
时,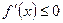 恒成立
恒成立
即 ,化简得
,化简得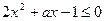 ,
,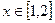
令 ,即
,即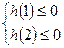 ,
,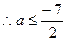 ………………………………4分
………………………………4分
(II)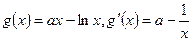 , …………………………………5分
, …………………………………5分
当 时,
时,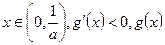 单调递减;
单调递减;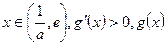 单调递增;
单调递增; 
当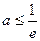 时,
时, 单调递减,
单调递减,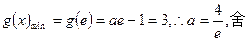
综上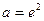 ………………………………8分
………………………………8分
(III)由(II)可知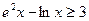
令 ,, …………………………………9分
,, …………………………………9分
当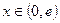 时,
时,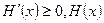 ,单调递增,
,单调递增, 
即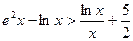 恒成立 …………………………………12分
恒成立 …………………………………12分
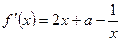 …………………………………1分
…………………………………1分 在
在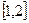 上单调递减,因此当
上单调递减,因此当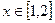
 时,
时,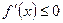 恒成立
恒成立即
 ,化简得
,化简得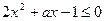 ,
,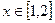
令
 ,即
,即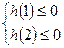 ,
,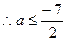 ………………………………4分
………………………………4分(II)
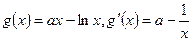 , …………………………………5分
, …………………………………5分当
 时,
时,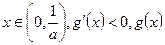 单调递减;
单调递减;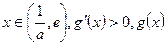 单调递增;
单调递增; 
当
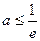 时,
时, 单调递减,
单调递减,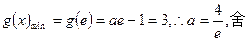
综上
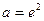 ………………………………8分
………………………………8分(III)由(II)可知
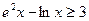
令
 ,, …………………………………9分
,, …………………………………9分当
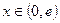 时,
时,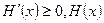 ,单调递增,
,单调递增, 
即
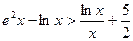 恒成立 …………………………………12分
恒成立 …………………………………12分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
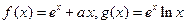 (
(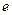 是自然对数的底数).
是自然对数的底数).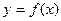 在
在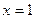 处的切线也是抛物线
处的切线也是抛物线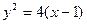 的切线,求
的切线,求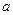 的值;
的值;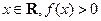 恒成立,试确定实数
恒成立,试确定实数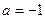 时,是否存在
时,是否存在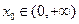 ,使曲线
,使曲线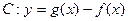 在点
在点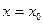 处的切线斜率与
处的切线斜率与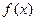 在
在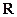 上的最小值相等?若存在,求符合条件的
上的最小值相等?若存在,求符合条件的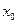 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.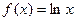
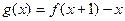 的最大值;
的最大值;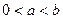 时,求证
时,求证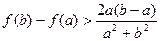 ;
;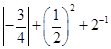 的结果相同的是( ).
的结果相同的是( ).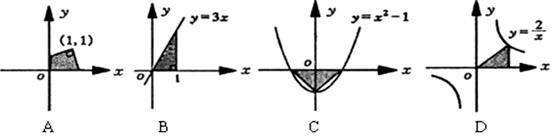
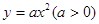 的两条切线互相垂直,则a为( )
的两条切线互相垂直,则a为( )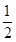
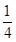
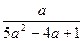 对称,求b的最小值.
对称,求b的最小值.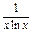 (x>0且x≠1).
(x>0且x≠1).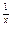 >xa对任意x∈(0,1)成立,求实数a的取值范围.
>xa对任意x∈(0,1)成立,求实数a的取值范围.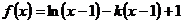
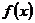 的单调区间和最大值;
的单调区间和最大值;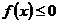 恒成立,求
恒成立,求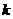 的取值范围;
的取值范围;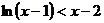 在
在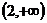 上恒成立;
上恒成立;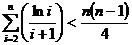
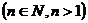
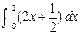 = .
= .