题目内容
10. 如图:在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,且C1B1⊥AB.
如图:在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,且C1B1⊥AB.(1)求证:CB⊥平面A1ABB1
(2)若C1B1=3,AB=4,∠ABB1=60°,求AC1与平面BCC1B1所成角的大小.
分析 (1)由已知得C1B1⊥AB,AB⊥BC,BC⊥BB1,由此能证明BC⊥平面A1ABB1.
(2)作出△ABB1的高AM,则AM⊥平面BCC1B1,连接AC1、C1M,则AM⊥C1M.AC1与平面BCC1所成角度就是AC1与平面BCC1B1所成角度,也就是∠AC1M.由此能求出AC1与平面BCC1B1所成角的大小.
解答  证明:(1)∵四边形BCC1B1是矩形,且C1B1⊥AB,
证明:(1)∵四边形BCC1B1是矩形,且C1B1⊥AB,
∴AB⊥BC,BC⊥BB1,AB∩BB1=B,
∴BC⊥平面A1ABB1.
解:(2)∵平面BCC1B1是矩形,C1B1⊥B1B,C1B1⊥AB,
∴C1B1⊥平面A1ABB1,则平面BCC1B1⊥平面A1ABB1.两平面的交线是BB1.∵A1ABB1是菱形,且∠ABB1=60°,∴△ABB1是等边三角形,
作出△ABB1的高AM,则AM⊥平面BCC1B1,
连接AC1、C1M,则AM⊥C1M.
AC1与平面BCC1所成角度就是AC1与平面BCC1B1所成角度,也就是∠AC1M.
由题设,在等边△ABB1中,B1M=MB=$\frac{AB}{2}$=2,AM=2$\sqrt{3}$,
在直角△C1B1M中,C1M=$\sqrt{4+9}$=$\sqrt{13}$,
在直角△AMC1中,tan∠AC1M=$\frac{AM}{{C}_{1}M}$=$\frac{2\sqrt{3}}{\sqrt{13}}$=$\frac{2\sqrt{39}}{13}$.
∴∠AC1M=arctan$\frac{2\sqrt{39}}{13}$.
∴AC1与平面BCC1B1所成角的大小为arctan$\frac{2\sqrt{39}}{13}$.
点评 本题考查线面垂直的证明,考查线面角的大粘的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | f(x)=x,g(x)=x2 | B. | f(x)=x,g(x)=$\root{3}{x^3}$ | C. | f(x)=x,g(x)=$\sqrt{x}$ | D. | f(x)=$\sqrt{x^2}g(x)=\sqrt{x}$ |
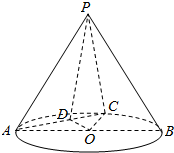 如图,在圆锥PO中,已知PO=$\sqrt{2}$,圆O的直径AB=2,C是弧AB的中点,D为AC的中点.
如图,在圆锥PO中,已知PO=$\sqrt{2}$,圆O的直径AB=2,C是弧AB的中点,D为AC的中点.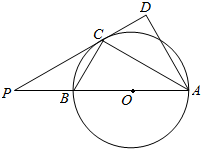 如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P.
如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P.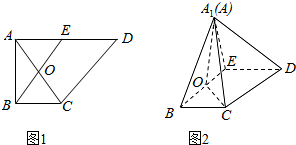 如图1,在直角梯形ABCD中,AD∥BC,AD⊥AB,AB=BC=$\frac{1}{2}$AD,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2,
如图1,在直角梯形ABCD中,AD∥BC,AD⊥AB,AB=BC=$\frac{1}{2}$AD,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2,