题目内容
已知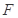 是
是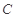 椭圆的一个焦点,
椭圆的一个焦点,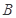 是短轴的一个端点,线段
是短轴的一个端点,线段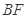 的延长线交
的延长线交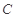 于点
于点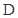 ,且
,且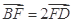 ,则
,则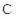 的离心率为 .
的离心率为 .
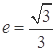
解析试题分析:设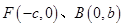 ,由
,由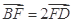 知点
知点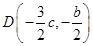 在椭圆上,代入椭圆方程
在椭圆上,代入椭圆方程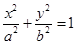 得
得 ,解得
,解得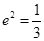 ,所以
,所以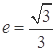 .
.
考点:椭圆的性质、离心率的求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
已知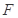 是
是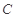 椭圆的一个焦点,
椭圆的一个焦点,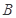 是短轴的一个端点,线段
是短轴的一个端点,线段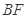 的延长线交
的延长线交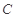 于点
于点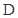 ,且
,且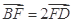 ,则
,则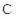 的离心率为 .
的离心率为 .
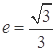
解析试题分析:设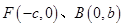 ,由
,由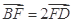 知点
知点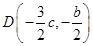 在椭圆上,代入椭圆方程
在椭圆上,代入椭圆方程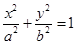 得
得 ,解得
,解得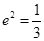 ,所以
,所以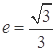 .
.
考点:椭圆的性质、离心率的求法.

 阅读快车系列答案
阅读快车系列答案