题目内容
4.高一年级下学期进行文理分班,为研究选报文科与性别的关系,对抽取的50名同学调查得到列联表如下,已知P(k2≥3.84)≈0.05,(k2≥5.024)≈0.025,计算k2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$≈4.848,则至少有95%的把握认为选报文科与性别有关.
分析 根据条件中所给的观测值,同所给的临界值进行比较,即可得出认为选修文科与性别有关系出错的可能性,即得认为选报文科与性别有关的概率.
解答 解:∵根据题意,得K2的观测值约为4.844,
且4.844>3.841,
∴认为选修文科与性别有关系出错的可能性为5%.
即至少有95%的把握认为选报文科与性别有关.
故答案为:95%.
点评 本题考查了独立性检验的应用,本题解题的关键是正确理解观测值对应的概率的意义,是基础题目.

练习册系列答案
相关题目
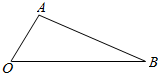 如图所示,在△AOB中,已知∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,则△AOC为钝角三角形的概率为$\frac{2}{5}$.
如图所示,在△AOB中,已知∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,则△AOC为钝角三角形的概率为$\frac{2}{5}$. 如图,在平行四边形ABCD中,∠BAD=120°,AB=2,AD=1,若$\overrightarrow{DE}=t\overrightarrow{DC}$,AE⊥BD,则实数t的值为$\frac{2}{5}$.
如图,在平行四边形ABCD中,∠BAD=120°,AB=2,AD=1,若$\overrightarrow{DE}=t\overrightarrow{DC}$,AE⊥BD,则实数t的值为$\frac{2}{5}$.