题目内容
1.囧函数y=$\frac{b}{|x|-a}$(a>0,b>0)的图象酷似汉字中的“囧”字,我们称其为“囧函数”.囧函数y=ax+$\frac{b}{x}$(a>0,b≠0)的图象类似“对勾函数”,对于两个简单的“囧函数”f(x)=$\frac{1}{|x|-1}$和“对勾函数”g(x)=x+$\frac{1}{x}$,下列叙述中正确的是①③④.①f(x)是偶函数,g(x)是奇函数;②f(x)既有极大值,也有极小值;③g(x)既有极大值,也有极小值;④两个图象有且仅有2个公共点.
分析 作出两个函数的图象f(x)=$\frac{1}{|x|-1}$的图象(绿色曲线),g(x)=x+$\frac{1}{x}$的图象(红色曲线),由图象可知答案.
解答 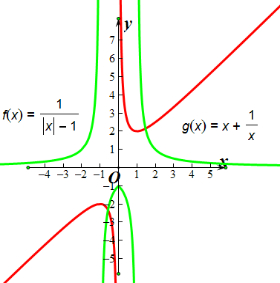 解:作出两个函数的图象f(x)=$\frac{1}{|x|-1}$的图象(绿色曲线),g(x)=x+$\frac{1}{x}$的图象(红色曲线),
解:作出两个函数的图象f(x)=$\frac{1}{|x|-1}$的图象(绿色曲线),g(x)=x+$\frac{1}{x}$的图象(红色曲线),
由图象知f(x)是偶函数,g(x)是奇函数;
f(x)既没有极大值,也没有极小值,
g(x)既有极大值,也有极小值;
两个图象有且仅有2个公共点.
故答案为:①③④.
点评 本题考查“囧函数”和“对勾函数”的新定义,关键要读懂题意,只要画出其图象就很容易求解了,解题过程中用到了数形结合的方法,属于基础题.

练习册系列答案
相关题目
12.在如图所示的程序框图中,若输出的S=9,则n=( )


| A. | 101 | B. | 100 | C. | 99 | D. | 98 |
16.阅读如图所示的程序框图,输出S的值是( )


| A. | 0 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{2}$ |
6.设a=2-1,b=log3$\frac{7}{81}$,c=($\frac{2}{3}$)-1,则( )
| A. | a>b>c | B. | b<a<c | C. | a<b<c | D. | b<c<a |
13.cos80°cos130°-sin80°sin130°等于( )
| A. | -$\frac{{\sqrt{3}}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
10.点A(1,2,3)关于xOy平面对称的点B坐标是( )
| A. | (-1,2,3) | B. | (1,-2,3) | C. | (1,2,-3) | D. | (-1,-2,3) |