题目内容
20.已知扇形AOB,点C在弧AB上(异于A,B两点),线段AB与OC交与点M,设$\overrightarrow{OC}=t\overrightarrow{OA}+3t\overrightarrow{OB}({t≠0})$,$\overrightarrow{AM}=m\overrightarrow{AB}({m≠0})$,则m=$\frac{3}{4}$.分析 根据条件及向量加法、减法,及数乘的几何意义及其运算便可得到$\overrightarrow{OM}=(1-m)\overrightarrow{OA}+m\overrightarrow{OB}$,从而有$\overrightarrow{OC}=k\overrightarrow{OM}=k(1-m)\overrightarrow{OA}+km\overrightarrow{OB}$,由平面向量基本定理便得到$\left\{\begin{array}{l}{k(1-m)=t}\\{km=3t}\end{array}\right.$,解出m即可.
解答 解:如图,$\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{AM}$=$\overrightarrow{OA}+m\overrightarrow{AB}$=$\overrightarrow{OA}+m(\overrightarrow{OB}-\overrightarrow{OA})$=$(1-m)\overrightarrow{OA}+m\overrightarrow{OB}$;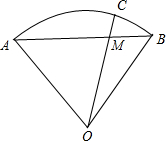
O,M,C三点共线;
∴存在实数k,$\overrightarrow{OC}=k\overrightarrow{OM}$=$k(1-m)\overrightarrow{OA}+mk\overrightarrow{OB}$;
又$\overrightarrow{OC}=t\overrightarrow{OA}+3t\overrightarrow{OB}$;
∴$\left\{\begin{array}{l}{k(1-m)=t}\\{mk=3t}\end{array}\right.$;
解得$m=\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 考查向量加法、减法,及数乘的几何意义及其运算,平面向量基本定理,以及共面向量基本定理.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案①方向相同的向量叫相等向量;
②零向量的长度为0;
③共线向量是在同一条直线上的向量;
④零向量是没有方向的向量;
⑤共线向量不一定相等;
⑥平行向量方向相同.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | (-∞,0]∪[1,+∞) | B. | (0,1) | C. | [0,1] | D. | (-∞,0)∪(1,+∞) |
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(2)利用(1)中的回归方程,预测该地区2015年农村居民家庭人均纯收入.
附:用最小二乘法求线性回归方程系数公式 $\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$.
| A. | 3 | B. | -3 | C. | 3i | D. | -3i |