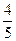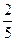题目内容
在平面直角坐标系中,已知点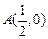 ,向量
,向量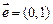 ,点B为直线
,点B为直线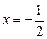 上的动点,点C满足
上的动点,点C满足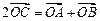 ,点M满足
,点M满足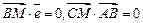 .
.
(1)试求动点M的轨迹E的方程;
(2)设点P是轨迹E上的动点,点R、N在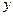 轴上,圆
轴上,圆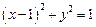 内切于
内切于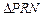 ,求
,求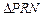 的面积的最小值.
的面积的最小值.
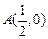 ,向量
,向量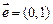 ,点B为直线
,点B为直线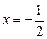 上的动点,点C满足
上的动点,点C满足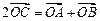 ,点M满足
,点M满足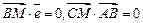 .
.(1)试求动点M的轨迹E的方程;
(2)设点P是轨迹E上的动点,点R、N在
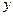 轴上,圆
轴上,圆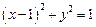 内切于
内切于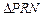 ,求
,求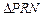 的面积的最小值.
的面积的最小值.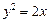 ,8
,8解:(1)设
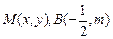 ,则
,则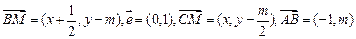 ,
,由
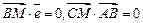 得
得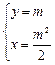 ,所以动点M的轨迹E的方程为
,所以动点M的轨迹E的方程为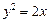 ;
;(2)设
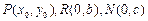 ,且
,且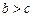 ,
,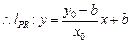 ,
,即
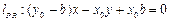 ,由相切得
,由相切得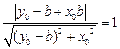 ,注意到
,注意到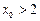 ,化简得
,化简得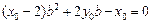 ,同理得
,同理得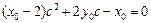 ,
,所以
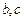 是方程
是方程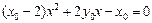 的两根,所以
的两根,所以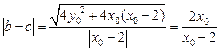 ,
,有
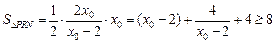 ,当
,当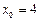 时
时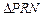 的面积的最小值为8.
的面积的最小值为8.
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
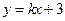 与圆
与圆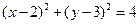 相交于M、N两点,若|MN|≥
相交于M、N两点,若|MN|≥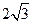 ,则
,则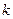 的取值范围是
的取值范围是




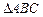 中,角
中,角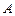 、
、 、
、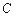 的对边分别为
的对边分别为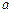 、
、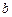 、
、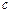 ,
,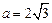 ,外接圆的圆心为
,外接圆的圆心为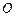 ,半径为
,半径为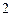 。
。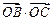 的值;
的值;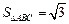 ,求
,求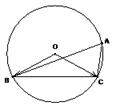
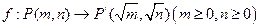 .设点
.设点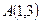 ,
,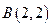 ,点M 是线段AB上一动点,
,点M 是线段AB上一动点,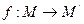 .当点M在线段AB上从点A开始运动到点B结束时,点M的对应点
.当点M在线段AB上从点A开始运动到点B结束时,点M的对应点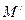 所经过的路线长度为 ()
所经过的路线长度为 ()



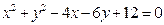 的圆心为C,点
的圆心为C,点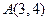 ,O为坐标原点.
,O为坐标原点.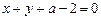 与圆
与圆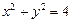 交于
交于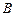 、
、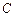 两点,
两点,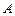 是圆上一点(与点
是圆上一点(与点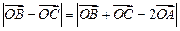 ,其中
,其中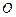 是坐标原点,则实数
是坐标原点,则实数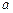 值是( )
值是( )



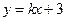 与圆
与圆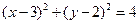 相交于M,N两点,若|MN|≥
相交于M,N两点,若|MN|≥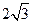 ,则
,则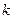 的取值范围是
的取值范围是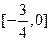



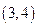 ,且与圆
,且与圆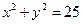 相切的直线的方程为 .
相切的直线的方程为 .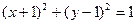 上一点P到直线
上一点P到直线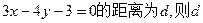 的最小值为 ( )
的最小值为 ( )