题目内容
(本小题满分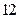 分)
分)
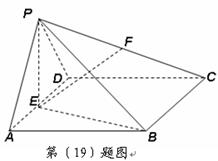
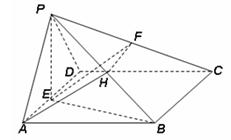
在四棱锥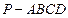 中,平面
中,平面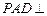 平面
平面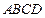 ,△
,△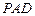 是等边三角形,底面
是等边三角形,底面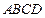 是边长为
是边长为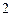 的菱形,
的菱形,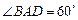 ,
,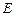 是
是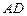 的中点,
的中点,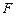 是
是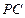 的中点.
的中点.
(Ⅰ)求证: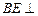 平面
平面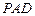 ;
;
(Ⅱ) 求证: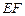 ∥平面
∥平面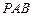 ;
;
(Ⅲ) 求直线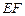 与平面
与平面 所成角的余弦值.
所成角的余弦值.
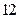 分)
分)在四棱锥
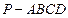 中,平面
中,平面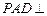 平面
平面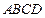 ,△
,△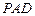 是等边三角形,底面
是等边三角形,底面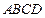 是边长为
是边长为 的菱形,
的菱形,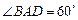 ,
,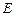 是
是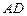 的中点,
的中点,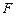 是
是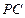 的中点.
的中点.
(Ⅰ)求证:
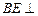 平面
平面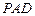 ;
;(Ⅱ) 求证:
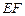 ∥平面
∥平面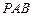 ;
;(Ⅲ) 求直线
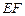 与平面
与平面 所成角的余弦值.
所成角的余弦值.略
(Ⅰ)∵E是AD中点,连结PE
∴AB=2,AE=1
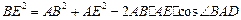
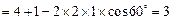
∴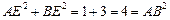
∴BE⊥AE
又平面PAD⊥平面ABCD,交线为AD,
∴BE⊥平面PAD,--------------4分
(Ⅱ) 取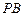 中点为
中点为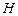 ,连结
,连结 ,
, ,
,
∵
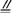
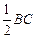 ,又∵
,又∵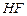 是△
是△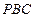 的中位线,
的中位线,
∴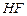
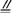
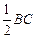 ,
,
∴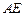
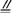
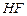 ,
,
∴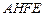 是平行四边形,
是平行四边形,
∴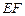 ∥
∥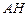 ,
,
又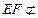 平面
平面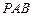 ,
,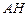
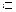 平面
平面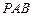 ,
,
∴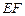 ∥平面
∥平面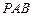 ;------------8分
;------------8分
(Ⅲ)由(Ⅰ)知,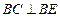 ,
,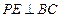 ,
,
又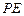 ,
,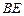 是平面
是平面 内两相交直线,
内两相交直线,
∴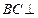 平面
平面 ,
,
又由(Ⅱ)知,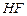 ∥
∥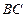 ,
,
∴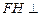 平面
平面 ,
,
∴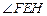 是直线
是直线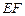 与平面
与平面 所成的角,
所成的角,
易知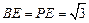 ,在
,在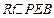 中,
中,
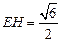 ,
,
∴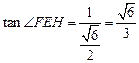 ,
,
∴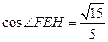 .
.
故直线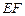 与平面
与平面 所成角的余弦值为
所成角的余弦值为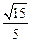 .--------12分
.--------12分
解法二:容易证明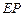 ,
,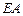 ,
,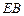 两两垂直,建立所示空间直角坐标系
两两垂直,建立所示空间直角坐标系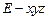 (如图).
(如图).
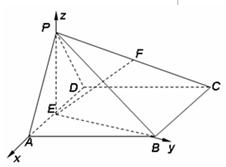
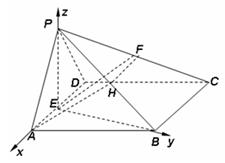
易求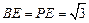 ,则
,则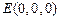 ,
,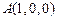 ,
,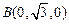 ,
,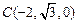 ,
,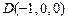 ,
,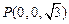 ,………2分,因为
,………2分,因为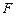 是
是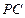 的中点,则
的中点,则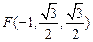 .---2分
.---2分
(Ⅰ)∵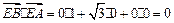 ,
,
∴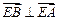 ,即
,即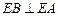 ,
,
∵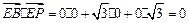 ,
,
∴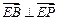 ,即
,即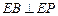 ,
,
∵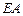 ,
,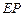 是平面
是平面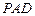 内的两相交直线,
内的两相交直线,
∴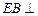 平面
平面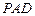 ;-----6分
;-----6分
(Ⅱ)取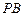 中点为
中点为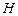 ,连结
,连结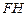 ,
,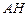 ,则
,则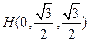 ,
,
∵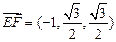 ,
,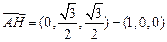
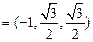 ,
,
∴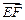 ∥
∥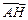 ,
,
∵又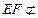 平面
平面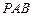 ,
,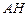
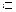 平面
平面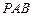 ,
,
∴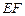 ∥平面
∥平面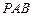 ;------------9分
;------------9分
(Ⅲ)∵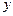 轴
轴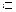 平面
平面 ,
,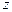 轴
轴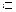 平面
平面 ,
,
∴ 平面 的法向量为
的法向量为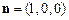 ,
,
∵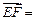
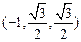 ,
,
设直线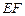 与平面
与平面 所成角为
所成角为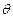 ,
,
∴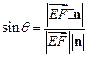
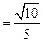 ,即
,即 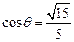 ,
,
故直线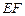 与平面
与平面 所成角的余弦值为
所成角的余弦值为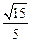 .-----12分
.-----12分
∴AB=2,AE=1
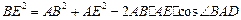
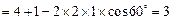
∴
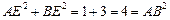
∴BE⊥AE
又平面PAD⊥平面ABCD,交线为AD,
∴BE⊥平面PAD,--------------4分
(Ⅱ) 取
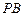 中点为
中点为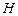 ,连结
,连结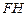 ,
,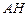 ,
,
∵
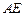
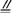
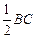 ,又∵
,又∵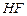 是△
是△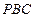 的中位线,
的中位线,∴
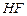
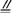
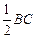 ,
,∴
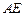
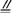
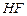 ,
,∴
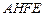 是平行四边形,
是平行四边形,∴
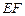 ∥
∥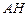 ,
,又
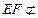 平面
平面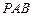 ,
,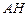
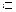 平面
平面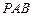 ,
,∴
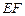 ∥平面
∥平面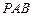 ;------------8分
;------------8分(Ⅲ)由(Ⅰ)知,
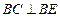 ,
,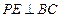 ,
,又
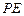 ,
,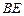 是平面
是平面 内两相交直线,
内两相交直线,∴
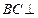 平面
平面 ,
,又由(Ⅱ)知,
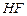 ∥
∥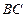 ,
,∴
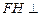 平面
平面 ,
,∴
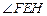 是直线
是直线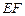 与平面
与平面 所成的角,
所成的角,易知
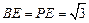 ,在
,在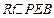 中,
中,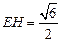 ,
,∴
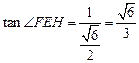 ,
,∴
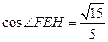 .
.故直线
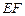 与平面
与平面 所成角的余弦值为
所成角的余弦值为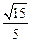 .--------12分
.--------12分解法二:容易证明
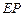 ,
,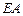 ,
,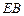 两两垂直,建立所示空间直角坐标系
两两垂直,建立所示空间直角坐标系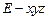 (如图).
(如图).

易求
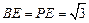 ,则
,则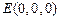 ,
,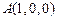 ,
,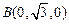 ,
,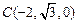 ,
,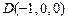 ,
,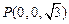 ,………2分,因为
,………2分,因为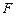 是
是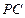 的中点,则
的中点,则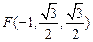 .---2分
.---2分(Ⅰ)∵
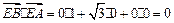 ,
,∴
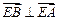 ,即
,即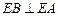 ,
,∵
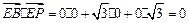 ,
,∴
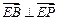 ,即
,即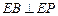 ,
,∵
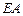 ,
,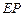 是平面
是平面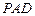 内的两相交直线,
内的两相交直线,∴
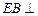 平面
平面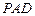 ;-----6分
;-----6分(Ⅱ)取
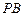 中点为
中点为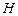 ,连结
,连结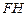 ,
,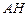 ,则
,则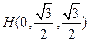 ,
,∵
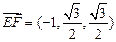 ,
,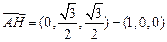
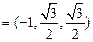 ,
,∴
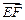 ∥
∥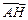 ,
,∵又
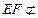 平面
平面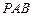 ,
,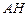
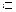 平面
平面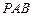 ,
,∴
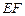 ∥平面
∥平面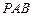 ;------------9分
;------------9分(Ⅲ)∵
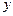 轴
轴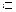 平面
平面 ,
,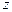 轴
轴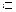 平面
平面 ,
,∴ 平面
 的法向量为
的法向量为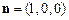 ,
,∵
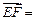
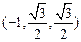 ,
,设直线
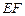 与平面
与平面 所成角为
所成角为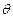 ,
,∴
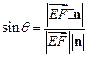
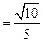 ,即
,即 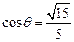 ,
,故直线
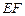 与平面
与平面 所成角的余弦值为
所成角的余弦值为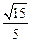 .-----12分
.-----12分
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
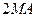 =
=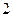

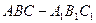 中,
中,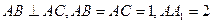 ,
,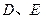 分别是
分别是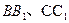 的中点,
的中点,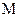 是
是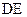 的中点.
的中点. 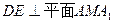 ;(2)求三棱锥
;(2)求三棱锥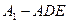 的体积;(3)求二面角
的体积;(3)求二面角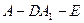 的余弦值.
的余弦值.
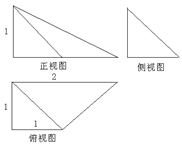
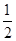
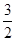

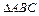 中,AB=2,BC=1,
中,AB=2,BC=1,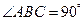 ,平面ABC外一点
,平面ABC外一点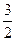 ,则三棱锥P—ABC的体积是( )
,则三棱锥P—ABC的体积是( )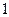
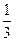
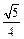
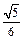
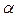 、
、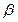 ,则下列命题中错误的是 ( )
,则下列命题中错误的是 ( )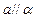 ,且
,且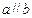 ,则
,则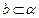 或
或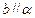
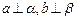 ,则
,则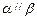
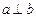 ,且
,且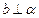
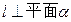 ,直线
,直线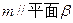 ,下列命题中正确的是( )
,下列命题中正确的是( )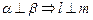
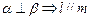
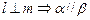
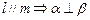
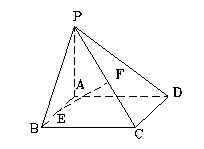 (1)求证:
(1)求证: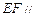 平面PAD;
平面PAD;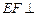 平面PCD.
平面PCD.