题目内容
【题目】已知函数g（x）满足g（x）=g′（1）ex﹣1﹣g（0）x+ 
，且存在实数x0使得不等式2m﹣1≥g（x0）成立，则m的取值范围为（ ）
A.（﹣∞，2]
B.（﹣∞，3]
C.[1，+∞）
D.[0，+∞）
【答案】C
【解析】解：∵g（x）=g′（1）ex﹣1﹣g（0）x+ 
，
∴g′（x）=g′（1）ex﹣1﹣g（0）+x，
∴g′（1）=g′（1）﹣g（0）+1，解得：g（0）=1，
g（0）=g′（1）e﹣1 ， 解得：g′（1）=e，
∴g（x）=ex﹣x+ 
x2 ，
∴g′（x）=ex﹣1+x，g″（x）=ex+1＞0，
∴g′（x）在R递增，而g′（0）=0，
∴g′（x）＜0在（﹣∞，0）恒成立，g′（x）＞0在（0，+∞）恒成立，
∴g（x）在（﹣∞，0）递减，在（0，+∞）递增，
∴g（x）min=g（0）=1，
若存在实数x0使得不等式2m﹣1≥g（x0）成立，
只需2m﹣1≥g（x）min=1即可，解得：m≥1，
故选：C．
分别求出g（0），g′（1），求出g（x）的表达式，求出g（x）的导数，得到函数的单调区间，求出g（x）的最小值，问题转化为只需2m﹣1≥g（x）min=1即可，求出m的范围即可．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】【2017湖南娄底二模】某种产品的质量以其质量指标值衡量，并依据质量指标值划分等级如下表：
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件，检测后得到如下的频率分布直方图：
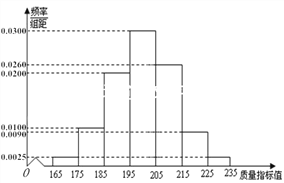
（Ⅰ）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定？
（Ⅱ）在样本中，按产品等级用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；
（Ⅲ）该企业为提高产品质量，开展了“质量提升月”活动，活动后在抽样检测，产品质量指标值
近似满足
，则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？
【题目】某媒体对“男女延迟退休”这一公众关注的问题进行了民意调查，如表是在某单位得到的数据（人数）：
（1）能否有90%以上的把握认为对这一问题的看法与性别有关？
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
（2）从赞同“男女延迟退休”16人中选出3人进行陈 述发言，求事件“男士和女士各至少有1人发言”的概率；
（3）若以这25人的样本数据来估计整个地区的总体数据，现从该地区（人数很多）任选5人，记赞同“男女延迟退休”的人数为X，求X的数学期望．
附：
p（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2= 
．
【题目】为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响，某农科所记录了5组昼夜温差与100颗种子发芽数，得到如表资料：
组号 | 1 | 2 | 3 | 4 | 5 |
温差x（°C） | 10 | 11 | 13 | 12 | 8 |
发芽数y（颗） | 23 | 25 | 30 | 26 | 16 |
该所确定的研究方案是：先从这五组数据中选取2组，用剩下的3组数据求出线性回归方程，再对被选取的2组数据进行检验．
（1）若选取的是第1组与第5组的两组数据，请根据第2组至第4组的数据，求出y关于x的线性回归方程 
；
（2）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（1）中所得的线性回归方程是否可靠？
（参考公式： 
= 
= 
， 
）
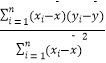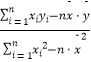