题目内容
设函数f(x)=ax-(k-1)a-x(a>0且a≠1)是定义域为R的奇函数.(1)求k值;
(2)若f(1)<0,试判断函数单调性并求使不等式f(x2+tx)+f(4-x)<0恒成立的t的取值范围;
(3)若f(1)=
 ,且g(x)=a2x+a-2x-2mf(x)在[1,+∞)上的最小值为-2,求m的值.
,且g(x)=a2x+a-2x-2mf(x)在[1,+∞)上的最小值为-2,求m的值.
【答案】分析:(1)根据奇函数的性质可得f(0)=0,由此求得k值.
(2)由f(x)=ax-a-x(a>0且a≠1),f(1)<0,求得1>a>0,f(x)在R上单调递减,不等式化为f(x2+tx)<f(x-4),即 x2+(t-1)x+4>0 恒成立,由<0求得t的取值范围.
(3)由f(1)= 求得a的值,可得 g(x)的解析式,令t=f(x)=2x-2-x,可知f(x)=2x-2-x为增函数,t≥f(1),令h(t)=t2-2mt+2,(t≥
求得a的值,可得 g(x)的解析式,令t=f(x)=2x-2-x,可知f(x)=2x-2-x为增函数,t≥f(1),令h(t)=t2-2mt+2,(t≥ ),分类讨论求出h(t)的最小值,再由最小值等于2,求得m的值.
),分类讨论求出h(t)的最小值,再由最小值等于2,求得m的值.
解答:解:(1)∵f(x)是定义域为R的奇函数,∴f(0)=0,…(2分)
∴1-(k-1)=0,∴k=2.…(4分)
(2)∵函数f(x)=ax-a-x(a>0且a≠1),
∵f(1)<0,∴a- <0,又 a>0,
<0,又 a>0,
∴1>a>0.…(6分)
由于y=ax单调递减,y=a-x单调递增,故f(x)在R上单调递减.
不等式化为f(x2+tx)<f(x-4).
∴x2+tx>x-4,即 x2+(t-1)x+4>0 恒成立,…(8分)
∴△=(t-1)2-16<0,解得-3<t<5.…(10分)
(3)∵f(1)= ,a-
,a-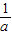 =
= ,即2a2-3a-2=0,∴a=2,或 a=-
,即2a2-3a-2=0,∴a=2,或 a=- (舍去).…(12分)
(舍去).…(12分)
∴g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2.
令t=f(x)=2x-2-x,由(1)可知k=2,故f(x)=2x-2-x ,显然是增函数.
∵x≥1,∴t≥f(1)= ,
,
令h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥ )…(15分)
)…(15分)
若m≥ ,当t=m时,h(t)min=2-m2=-2,∴m=2…(16分)
,当t=m时,h(t)min=2-m2=-2,∴m=2…(16分)
若m< ,当t=
,当t= 时,h(t)min=
时,h(t)min=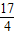 -3m=-2,解得m=
-3m=-2,解得m= >
> ,舍去…(17分)
,舍去…(17分)
综上可知m=2.…(18分)
点评:本题主要考查指数型复合函数的性质以及应用,函数的奇偶性的应用,以及函数的恒成立问题,属于中档题.
(2)由f(x)=ax-a-x(a>0且a≠1),f(1)<0,求得1>a>0,f(x)在R上单调递减,不等式化为f(x2+tx)<f(x-4),即 x2+(t-1)x+4>0 恒成立,由<0求得t的取值范围.
(3)由f(1)=
 求得a的值,可得 g(x)的解析式,令t=f(x)=2x-2-x,可知f(x)=2x-2-x为增函数,t≥f(1),令h(t)=t2-2mt+2,(t≥
求得a的值,可得 g(x)的解析式,令t=f(x)=2x-2-x,可知f(x)=2x-2-x为增函数,t≥f(1),令h(t)=t2-2mt+2,(t≥ ),分类讨论求出h(t)的最小值,再由最小值等于2,求得m的值.
),分类讨论求出h(t)的最小值,再由最小值等于2,求得m的值.解答:解:(1)∵f(x)是定义域为R的奇函数,∴f(0)=0,…(2分)
∴1-(k-1)=0,∴k=2.…(4分)
(2)∵函数f(x)=ax-a-x(a>0且a≠1),
∵f(1)<0,∴a-
 <0,又 a>0,
<0,又 a>0,∴1>a>0.…(6分)
由于y=ax单调递减,y=a-x单调递增,故f(x)在R上单调递减.
不等式化为f(x2+tx)<f(x-4).
∴x2+tx>x-4,即 x2+(t-1)x+4>0 恒成立,…(8分)
∴△=(t-1)2-16<0,解得-3<t<5.…(10分)
(3)∵f(1)=
 ,a-
,a-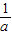 =
= ,即2a2-3a-2=0,∴a=2,或 a=-
,即2a2-3a-2=0,∴a=2,或 a=- (舍去).…(12分)
(舍去).…(12分)∴g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2.
令t=f(x)=2x-2-x,由(1)可知k=2,故f(x)=2x-2-x ,显然是增函数.
∵x≥1,∴t≥f(1)=
 ,
,令h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥
 )…(15分)
)…(15分)若m≥
 ,当t=m时,h(t)min=2-m2=-2,∴m=2…(16分)
,当t=m时,h(t)min=2-m2=-2,∴m=2…(16分)若m<
 ,当t=
,当t= 时,h(t)min=
时,h(t)min=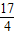 -3m=-2,解得m=
-3m=-2,解得m= >
> ,舍去…(17分)
,舍去…(17分)综上可知m=2.…(18分)
点评:本题主要考查指数型复合函数的性质以及应用,函数的奇偶性的应用,以及函数的恒成立问题,属于中档题.

练习册系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |