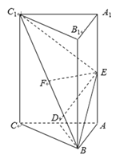
题目内容
【题目】四个同样大小的球![]() ,
,![]() ,
,![]() ,
,![]() 两两相切,点
两两相切,点![]() 是球
是球![]() 上的动点,则直线
上的动点,则直线![]() 与直线
与直线![]() 所成角的正弦值的取值范围为( ).
所成角的正弦值的取值范围为( ).
A.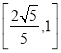 B.
B.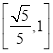 C.
C.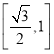 D.
D.
【答案】C
【解析】
三棱锥![]() 是正四面体,正四面体的对棱互相垂直,因此平移直线
是正四面体,正四面体的对棱互相垂直,因此平移直线![]() 至
至![]() 位置,则
位置,则![]() ,过
,过![]() 、
、![]() 的平面截球
的平面截球![]() 得一个大圆,过
得一个大圆,过![]() 作大圆的两条切线
作大圆的两条切线![]() 、
、![]() .当点
.当点![]() 运动至切点
运动至切点![]() 时,
时,![]() 最小,当点
最小,当点![]() 运动至切点
运动至切点![]() 时,
时,![]() 最大.分别求出角的最大值和最小值,再求正弦值即可.
最大.分别求出角的最大值和最小值,再求正弦值即可.
解:
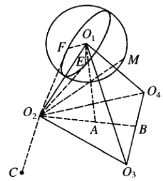
由四个同样大小的球![]() ,
,![]() ,
,![]() ,
,![]() 两两相切,
两两相切,
则可以把![]() ,
,![]() ,
,![]() ,
,![]() 看成正四面体的四个顶点,
看成正四面体的四个顶点,
球的半径为棱长的一半,记球的半径为1,则正四面体的棱长为2.
平移直线![]() 至
至![]() 位置,过
位置,过![]() ,
,![]() 的平面截球
的平面截球![]() 得一个大圆,
得一个大圆,
过![]() 作大圆的两条切线
作大圆的两条切线![]() ,
,![]() ,
,
由线面垂直易证![]() ,由图可知,
,由图可知,
当点![]() 运动至切点
运动至切点![]() 时,
时,![]() 最小,
最小,
当点![]() 运动至切点
运动至切点![]() 时,
时,![]() 最大,
最大,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,则
,则![]() ,
,
即直线![]() 与直线
与直线![]() 所成角
所成角![]() ,
,
则直线![]() 与直线
与直线![]() 所成角的正弦值的取值范围为
所成角的正弦值的取值范围为 .
.
故选:C.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目