题目内容
【题目】设数列![]()
![]() 是公差不为零等差数列,满足
是公差不为零等差数列,满足![]() ;数列
;数列![]()
![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)在![]() 和
和![]() 之间插入1个数
之间插入1个数![]() ,使
,使![]() 成等差数列;在
成等差数列;在![]() 和
和![]() 之间插入2个数
之间插入2个数![]() ,使
,使![]() 成等差数列;……;在
成等差数列;……;在![]() 和
和![]() 之间插入
之间插入![]() 个数
个数![]() ,使
,使![]() 成等差数列,
成等差数列,
(i)求![]() ;
;
(ii)是否存在正整数![]() ,使
,使![]() 成立?若存在,求出所有的正整数对
成立?若存在,求出所有的正整数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1) (2)
(2)![]() (i)(ii)
(i)(ii)![]() 及
及![]() .
.
【解析】
(1)设数列![]() 的公差为
的公差为![]() ,将已知条件用
,将已知条件用![]() 表示,解方程组,即可求出
表示,解方程组,即可求出![]() ;令
;令![]() ,得出
,得出![]() 为等比数列,即可求出通项;
为等比数列,即可求出通项;
(2)(i)由题意![]() 成等差数列,求出
成等差数列,求出![]() 的通项公式,进而求出
的通项公式,进而求出![]() 就为数列
就为数列![]() 的前
的前![]() 项和,利用错位相减法即可求解;
项和,利用错位相减法即可求解;
(ii)根据已知得出![]() 的函数关系,利用
的函数关系,利用![]() ,结合函数值的变化,即可求解.
,结合函数值的变化,即可求解.
(1)设数列![]() 的公差为
的公差为![]()
则由条件![]() ,
,
可得![]() ,
,![]() ,
,
又由![]() ,
,
可得![]() ,
,
将![]() 代入上式得
代入上式得![]() ,
,
![]()
![]()
由![]() ①
①
当![]() 时,
时,![]() ②
②
①-②得:![]()
![]()
又![]()
![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
故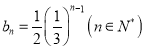
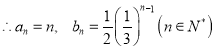
(2)①在![]() 和
和![]() 之间插入
之间插入![]() 个数
个数![]() ,
,
因为![]() 成等差数列,设公差为
成等差数列,设公差为![]()
则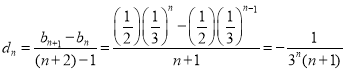 ,
,
则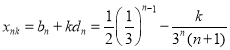 ,
,
 ,
,
![]() ①
①
则![]() ②
②
①-②得: ,
,
![]()
②若![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
则![]() ,
,
![]() ,
,
从而![]() ,
,
故 ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
下证![]() 时,有
时,有![]() ,
,
即证![]() ,
,
设![]() ,
,
则![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,
故![]() 时,
时,![]()
即![]() ,
,
从而![]() 时,
时,![]() 不是整数
不是整数
故所求的所有整数对为![]() 及
及![]() .
.

【题目】哈三中团委组织了“古典诗词”的知识竞赛,从参加考试的学生中抽出60名学生(男女各30名),将其成绩分成六组![]() ,
,![]() ,…,
,…,![]() ,其部分频率分布直方图如图所示.
,其部分频率分布直方图如图所示.
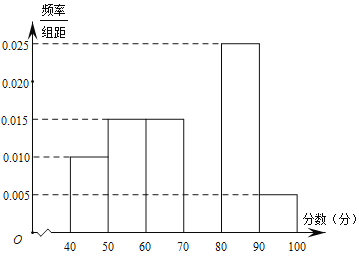
(Ⅰ)求成绩在![]() 的频率,补全这个频率分布直方图,并估计这次考试的众数和中位数;
的频率,补全这个频率分布直方图,并估计这次考试的众数和中位数;
(Ⅱ)从成绩在![]() 和
和![]() 的学生中选两人,求他们在同一分数段的概率;
的学生中选两人,求他们在同一分数段的概率;
(Ⅲ)我们规定学生成绩大于等于80分时为优秀,经统计男生优秀人数为4人,补全下面表格,并判断是否有99%的把握认为成绩是否优秀与性别有关?
优秀 | 非优秀 | 合计 | |
男 | 4 | 30 | |
女 | 30 | ||
合计 | 60 |
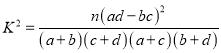
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
【题目】甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级 | 参赛人数 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 45 | 83 | 86 | 85 | 82 |
乙 | 45 | 83 | 84 | 85 | 133 |
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛得分![]() 分为优秀);
分为优秀);
③甲、乙两班成绩为85分的学生人数比成绩为其他值的学生人数多;
④乙班成绩波动比甲班小.
其中正确结论有( )
A.1个B.2个C.3个D.4个
【题目】在“创文创卫”活动中,某机构为了解一小区成年居民“吸烟与性别”是否有关.从该小区中随机抽取200位成年居民,得到下边列联表:已知在全部200人中随机抽取1人,抽到不吸烟的概率为0.75.
吸烟 | 不吸烟 | 合计 | |
男 | 40 | ||
女 | 90 | ||
合计 | 200 |
(1)补充上面的列联表,并判断:能否有99.9%的把握认为“吸烟与性别”有关;
(2)用分层抽样的方法从吸烟居民中选5人出来,然后再从中抽2人出来,给小区居民谈谈吸烟的危害性,求恰好抽到“一男一女”的概率.
参考公式: 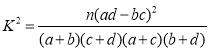 .
.
参考数据:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |



