题目内容
若 ,函数
,函数 在
在 处有极值,则
处有极值,则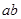 的最大值是( )
的最大值是( )
| A.9 | B.6 | C.3 | D.2 |
A
解析试题分析:求出导函数,利用函数在极值点处的导数值为0得到a,b满足的条件,利用基本不等式求出ab的最值解:由题意,求导函数f′(x)=12x2-2ax-2b,∵在x=1处有极值,∴a+b=6,∵a>0,b>0,∴ab≤(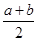 )2=9,当且仅当a=b=3时取等号,以ab的最大值等于9,答案为A
)2=9,当且仅当a=b=3时取等号,以ab的最大值等于9,答案为A
考点:基本不等式
点评:本题考查函数在极值点处的导数值为0、考查利用基本不等式求最值,需注意:一正、二定、三相等.

练习册系列答案
相关题目
下列结论正确的是( )
A.当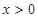 且 且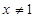 时, 时,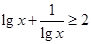 ; ; | B.当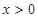 时, 时,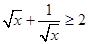 ; ; |
C.当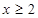 时, 时,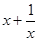 的最小值为2; 的最小值为2; | D.当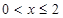 时, 时,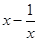 无最大值; 无最大值; |
设 的最小值是( )
的最小值是( )
| A.10( | B. | C. | D. |
已知正实数 ( )
( )
| A.6 | B.8 | C.9 | D.16 |
设x>0,y>0,x+y+xy=2,则x+y的最小值是( )
A.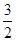 | B.1 + 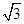 | C.2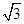 -2 -2 | D.2-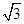 |
设 ,则
,则 三数中( )
三数中( )
| A.至少有一个不大于2 | B.都小于2 |
| C.至少有一个不小于2 | D.都大于2 |
如果 ,那么
,那么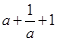 的最小值是( )
的最小值是( )
| A.2 | B.3 | C.4 | D.5 |
下列命题中正确的是 ( )
A. 的最小值是2 的最小值是2 | B. 的最小值是2 的最小值是2 |
C. 的最小值是 的最小值是 | D. 的最大值是 的最大值是 |
设正实数 满足
满足 ,则当
,则当 取得最大值时,
取得最大值时, 的最大值为( )
的最大值为( )
A. | B. | C. | D. |