题目内容
【题目】已知动圆M与圆C1：（x+4）2+y2=2外切，与圆C2：（x﹣4）2+y2=2内切，求动圆圆心M的轨迹方程．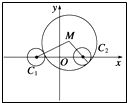 
【答案】解：设动圆圆心M（x，y），半径为r，∵圆M与圆C1：（x+4）2+y2=2外切，与圆C2：（x﹣4）2+y2=2内切，
∴|MC1|=r+ 
，|MC2|=r﹣ ，
∴|MC1|﹣|MC2|=2 ＜8，
由双曲线的定义，可得a= ，c=4；则b2=c2﹣a2=14；
∴点M的轨迹是以点C1 ， C2为焦点的双曲线的一支，
∴动圆圆心M的轨迹方程： 
﹣ 
【解析】根据两圆外切和内切的判定，圆心距与两圆半径和差的关系，设出动圆半径为r，消去r，根据圆锥曲线的定义，即可求得动圆圆心M的轨迹，进而可求其方程．
【考点精析】通过灵活运用双曲线的概念，掌握平面内与两个定点
，
的距离之差的绝对值等于常数（小于
）的点的轨迹称为双曲线．这两个定点称为双曲线的焦点，两焦点的距离称为双曲线的焦距即可以解答此题．
练习册系列答案
春雨教育同步作文系列答案
相关题目
