题目内容
某中学经市批准建设分校,工程从2010年底开工到2013年底完工,分三期完成,经过初步招标淘汰后,确定由甲、乙两建筑公司承建,且每期工程由两公司之一独立完成,必须在建完前一期工程后再建后一期工程,已知甲公司获得第一期,第二期,第三期工程承包权的概率分别是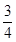 ,
,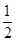 ,
,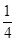 .
.
(I)求甲乙两公司均至少获得l期工程的概率;
(II)求甲公司获得的工程期数的分布列和数学期望E(X).
(I)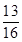 ;
;
(II)分布列为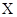
0 1 2 3 
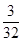
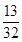
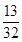
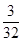
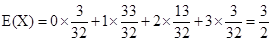 .
.
解析试题分析:(I)由题意得乙公司得第一期,第二期,第三期工程承包权的概率分别是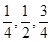 .记“甲乙至少获得1期工程”为事件
.记“甲乙至少获得1期工程”为事件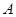 ,甲公司获得1期工程,乙公司获得2期工程为事件
,甲公司获得1期工程,乙公司获得2期工程为事件 ,甲公司获得2期工程,乙公司获得1期工程为事件
,甲公司获得2期工程,乙公司获得1期工程为事件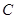 .
.
利用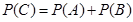 或
或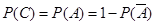 加以计算;
加以计算;
(II)由题意知,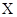 可取
可取 ,
,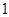 ,
,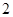 ,
,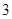 .利用相互独立事件同时发生的概率计算公式即得.
.利用相互独立事件同时发生的概率计算公式即得.
应用数学期望计算公式得 .
.
此类问题的解答,关键在于明确算理,细心计算.
试题解析:(I)由题意得乙公司得第一期,第二期,第三期工程承包权的概率分别是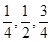 .记“甲乙至少获得1期工程”为事件
.记“甲乙至少获得1期工程”为事件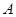 ,甲公司获得1期工程,乙公司获得2期工程为事件
,甲公司获得1期工程,乙公司获得2期工程为事件 ,甲公司获得2期工程,乙公司获得1期工程为事件
,甲公司获得2期工程,乙公司获得1期工程为事件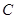 .
.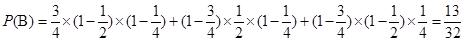 ,
,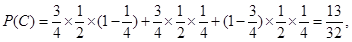
所以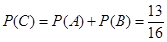
或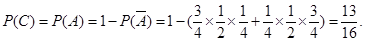
(II)由题意知,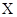 可取
可取 ,
,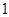 ,
,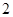 ,
,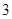 .
.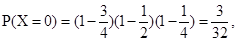
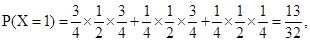
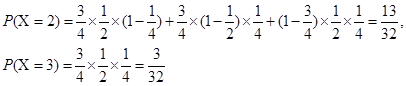
分布列为
所以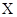

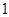
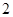
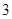

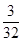
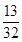
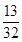
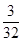
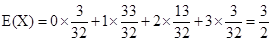 .
.
考点:相互独立事件同时发生的概率,对立事件的概率,随机变量的分布列及数学期望.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
为了参加2013年市级高中篮球比赛,该市的某区决定从四所高中学校选出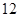 人组成男子篮球队代表所在区参赛,队员来源人数如下表:
人组成男子篮球队代表所在区参赛,队员来源人数如下表:
| 学校 | 学校甲 | 学校乙 | 学校丙 | 学校丁 |
| 人数 | 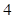 | 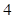 | 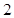 | 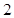 |
(Ⅰ)求这两名队员来自同一学校的概率;
(Ⅱ)设选出的两名队员中来自学校甲的人数为
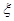 ,求随机变量
,求随机变量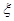 的分布列及数学期望
的分布列及数学期望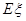 .
. 某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
| | 围棋社 | 舞蹈社 | 拳击社 |
| 男生 | 5 | 10 | 28 |
| 女生 | 15 | 30 | m |
(Ⅰ)求拳击社团被抽出的6人中有5人是男生的概率;
(Ⅱ)设拳击社团有X名女生被抽出,求X的分布列及数学期望
 .
. 
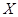 ,求随机变量
,求随机变量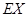 .
. .
.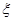 ,试写出
,试写出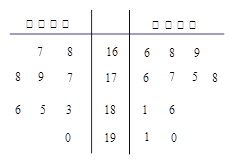
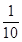 和p.
和p.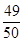 ,求p的值;
,求p的值;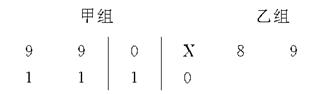
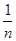 [(x1-
[(x1- )2+(x2-
)2+(x2-