题目内容
若a、b、c都是小于1的正数，求证：(1－a)b，(1－b)c，(1－c)a三个数不可能同时大于
．
答案：
解析：
提示：
解析：
|
分析：本题为“不可能”问题，常常用反证法． 证明：假设(1－a)b，(1－b)c，(1－c)a都大于 即(1－a)b＞ ∵a、b、c都是小于1的正数，0＜1－a＜1，0＜1－b＜1，0＜1－c＜1． ∴ ∴1＜1－a＋b，即a＜b． ∴1＜1－b＋c，即b＜c． ∴a＜c． ∴1＜1－c＋a，即c＜a与a＜c矛盾． ∴假设不成立． ∴(1－a)b、(1－b)c、(1－c)a三个数不可能同时大于 |
，
＜(1－a)b＜(
)2．
)2，
)2，提示：
|
用反证法证明问题时，所得到的结论有可能与某个已知条件相矛盾，也有可能与某事实相矛盾，也可能证明过程中自相矛盾． |
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目
．
.
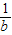，b+
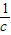，c+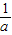
三数中至少有一个不小于2”，提出的假设是（ ）
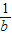，b+
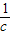，c+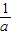
至少有一个小于2
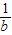，b
，c+
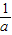都小于2